|
The German cipher machine EnigmaThis webpage was created after an interesting study tour to London and Bletchley Park. As a high school teacher and mathematician from Denmark, I normally only write in my native language, which is Danish. This time, however, I have decided to tell a story about the German ciphermachine Enigma in English too, because of several reasons. Firstly I am grateful to Chris Christensen and MAA for giving me the permission to place an article about the Polish contributions to the solution of Enigma on my website and because of the kindness I received from the people from Bletchley Park, who arranged our visit and who have provided me with a few historic photos from Bletchley Park! I can be contacted on e-mail: Erik Vestergaard. Notice that in many occasions clicking an image yields an enlarged version!
1. IntroductionThe last week of September 2007 I was on a study tour to London together with one of my colleagues and my dear class 3F from Haderslev Katedralskole, a high school in Denmark. One of the academic items was a visit at Bletchley Park, situated 90 kilometres north west of London - a 45 minutes trip by train from Euston Station in central London. Our goal was to experience how the famous code breakers at Bletchley Park back in 1939-45 made a big difference in the War by solving the German cipher machine Enigma and to learn about the mathematics involved.
The story about Enigma is a fascinating one. Not until 1974 was it revealed for the public that the German crypto machine had been broken not only a few times, but intensively during World War II. Since then many books have been written explaining what took place during those critical years including the role of Enigma, and several movies have appeared too. The Germans regarded their machine as unbreakable, and it is an extraordinary achievement that ingenious mathematicians and other people with special ability were able to break it. Maybe it was the fear and the necessity to solve it, which drove the Allied and made them succeed in this major task, as indicated by Simon Singh in his book The Code Book. In a later section we will look closer at our visit at Bletchley Park. First, however, let's start with the history of cryptography. I will get back to our visit in section 14.
2. The situation before Enigma - history brieflyOne of the simplest ciphers are the so-called monoalphabetic substitution ciphers, in which every letter in the plain-text (the original text) is substituted with another letter from the same alphabet, making it apparently unreadable. However it was early on discovered to be a poor cipher, because statistics can be applied: Depending on the language, some letters will occur with much higher frequency than other letters. In English for example, an e is much more frequent occurring than a k in most texts. Because the letter e has the highest frequency of all letters in most English texts, there is a high probability that the letter occurring most frequently in a specific crypto-text (encrypted text) is in fact a substitution for an e. In a similar way using statistics on the remaining letters it is usually possible to find the other substitutions as well. This procedure usually works if the encrypted text has a certain length, because the frequencies then will tend to approach the frequencies of an “average English text”. To “repair” the weaknesses of a monoalphabetic cipher, the concept of a polyalphabetic substitution cipher was introduced. The first polyalphabetic system seems to be due to Leon Battista Alberti around 1467, according to Wikipedia, but the best known example is probably the so-called Vigenère cipher. Here more than one alphabet were being used, that way limiting the success of statistics being invoked. The use of many alphabets has a tendency to level out the frequencies for the letters in the encrypted text, thereby hiding their origin. However even in this case the code breakers had an answer if the number of different alphabets used is not too large. Kasiski and Friedman applied statistics in a very ingenious way to decrypt the code. However it is a well-known fact that when using a new alphabet for every letter being encrypted yields an unbreakable cipher - if there is no system in the alphabets being applied! The problem with that kind of cipher is however that it is impracticable. Such a cipher has been used sometimes in the history, but only on a few occasions, because it requires a large codebook containing information of every alphabet used. It also takes a long time to decrypt. During wars with thousands of messages being sent every day, each message containing maybe 300 letters, it is not applicable. Therefore after World War I people looked for ways to mechanize encryption. One of the solutions was an electro-mechanical device named Enigma designed by the German electrical engineer Arthur Scherbius and patented in 1918. It was initially not created as a device for use at war, rather as a device to secure information and transactions in commercial businesses, like in banks. But war was approaching and the German military adopted the machine, while improving its security. The ground was paved for a new kind of technology being used at war ...
3. How Enigma worksIn this section we will be dealing with the function of Enigma and only occasionally go into the history of this machine, postponing it to subsequent sections. The picture below is showing an Enigma machine from Bletchley Park. At the top the three wheels or rotors are showing through the black cover, covering the interior of the machine. Just below the wheels you see the lampboard and below it the keyboard. In front is shown the plugboard with plugs connecting different letters. A better close-up of the plugboard:
Ring settings
|
|
|
|
Marian Rejewski in 1943 or 1944 |
In the following let's look at how the Germans encrypted their messages during World War II using Enigma. It is important to emphasize that there was not just one single procedure! In fact the German Navy (Kriegsmarine) from 1942 and on even used a special version of Enigma containing four wheels, whereas the German Army (Wehrmacht) and German Airforce (Luftwaffe) used the three wheel version of Enigma as described above. Even within the different units or networks of the German military, different keys and procedures were being applied. For example the German High Command (Oberkommando) did not use the same daily keys (see below) as did the ordinary German Army. That way the Germans prevented information addressed for one part of the military to be read by other parts of the German military. In addition it made it more difficult for the enemy to break the codes! Another complication in understanding the Enigma traffic is the fact that things changed during the course of the war. In short: When the Germans sensed any weaknesses, they changed procedures!
In order for the German receivers to be able to decrypt an encrypted text, which the enemy was not supposed to be able to do, the German receivers needed additional information. This was provided through a codebook or a monthly list of daily keys, distributed under high security to all the relevant German participants in the war: The German Army (Wehrmacht), the German Navy (Kriegsmarine), the German Airforce (Luftwaffe), the German High Command (Oberkommando), etc. Remember however that the different units or networks in the German military did not all receive the same lists! As mentioned the monthly lists contained the socalled daily keys, but also the socalled Kenngruppen to identify the kind of key being used. Below is an illustration on a possible monthly list for the Army-Staff (Armee-Stab). It contains fictitious values but the form is perfectly realistic. If you want to see authentic real World War II monthly lists, please look on this page: http://cryptocellar.org/Enigma/). Click on the image for an enlarged version.
Let's say that you are an operator in the German Army and want to send the message Wir werden Morgen um 3 Uhr Nachmittags die Truppen angreifen to another unit in the German Army on the 29th of June 1943. Then you would look up in your monthly list to find the daily key for the 29th of June 1943:
|
Rotor arrangement (Walzenlage): I, III, II Ring settings (Ringstellung): B R E (or in numbers 02 18 05). Plugboard settings (Steckerverbindungen): AR DQ LP MF ES KT YZ HW CO UG |
(NB! The meaning of the letters L, M and N are explained in section 3 above).
The daily key provides you with part of the information on how to set up your Enigma machine. It is here assumed that you are using the reflector (Umkehrwalze) named B. Before you can go on applying Enigma, you need the rotor settings (Grundstellung). Here you are allowed to choose a three letter combination at random, say ISL. This means that when starting the encryption, wheel L (here I) has the letter I on top, wheel M (here III) has letter S on top and wheel N (here II) has letter L on top. In the following we will call this the indicator setting (same as Grundstellung).
Now you need something to encrypt! Here again you are choosing a three letter combination completely on your own. Let's say you choose the letters ETG. They are supposed to be the message key, that is some other rotor settings we will be using later on. For now, however, just forget about what it means and just type the three letters in on your Enigma machine using the settings given by the daily key and the indicator setting described above. You will get AWB as the encrypted letters.
You are now ready to carry out your main job, which is to encrypt your plain text. First you adjust the three rotors according to the letters in the message key: E, T and G and keep the other Enigma settings identical to the ones used during the first encryption! Then you simply type W, I, R, W, E, R, D, E, N, M, etc., thereby getting the encrypted letters J, M, B, O, P, etc. The encrypted letters are being placed in groups of five for better readability. You are encouraged to test this encryption process using Dirk Rijmenants excellent Enigma simulator mentioned in section 15. There is a link to Dirk's site, from which you can download the program for free.
|
Message key Rotor settings: E T G |
The encoding operator need to tell the receiving operator which kind of key is being used. It wouldn't work if a Navy operator tried reading an Army encrypt! Different types of Enigma trafic should be separated. The kind of key can be identified through just one of the trigrams placed under the name Kenngruppen for the actual day in the monthly list. For the 29th of June, the Kenngruppen contains the four trigrams: HAX, OQA, KPA and YYT. You can choose any of them, say KPA. To make it look better - and maybe to confuse the enemy - you put two random letters in front of KPA, say UK, making it into a five letter group: UKKPA. This group is finally placed in front of the other five letter groups constituting the main encrypt. It should be mentioned that a permutation of the letters in the trigram is allowed, so PAK would be accepted. Below is an illustration visualizing our procedure so far.
Two other items needed for a receiving operator are the indicator setting ISL and the result of the first encryption, the encrypted messenge key, AWB. This information would be provided in an unenciphered preample. Along with this information other important or useful information was typically placed in the preample, like for example: The callsigns of the radio stations involved (first the sending station, then the destination(s)), the time of origin of the message, the number of letters in the text (including the first five letter group), an indication whether the message was complete or was a part of a bigger message. So our complete message send by morse signals could read something like the following:

Although it is not relevant in this example, it has to be mentioned, that if the plain text exceeded 250 letters, the message should be divided into parts of at most 250 letters, with each of the parts encrypted using different indicator settings and message keys. This precaution was taken by the Germans to prevent the problem called depth, which means that if an enemy has enough statistical data - with the same Enigma settings - it might be able to use it to break the code! Let's summarize the procedure for the encoding operator as explained above:
Notice that the Germans usually typed in the message leaving no spaces - spaces would help a lot in breaking the code. There excisted however special letter combinations to account for abbreviations, numbers etc. It will go too far to explain this here. It has to be pointed out that the above procedure is typical for Army messages after May 1940, but quite different from the procedure used to encrypt Navy messages. Those were much more advanced. No more about this here.
Now you might wonder how a receiving German operator would handle the encrypted message described above? First he would recognice from the last three letters in the Letter Identification Group (Buchstabenkenngruppe), KPA, that the message was intended for him, and he would know which monthly list to apply! Next he would do the following to decipher the message:
Now that you have heard about the procedure used by the German Army and Air Force after May 1940 you may wonder how the situation was before this date, when Marian Rejewski was making his great contributions. There were a few differences. Firstly the message key was being encrypted twice!
The reason for doing so was pure care taken by the Germans: It made the receiving operator more sure he received the correct message key: When decrypting AWBUUK he got ETGETG instead of just decrypting AWB into ETG. Finding ETG appearing twice made him more sure nothing had been screwed up in the reception of the radio signals - sometimes signals were garbled under transmission and handling. This habit of encrypting the message key twice was however a severe weakness, and it was exploited to the fullest by Marian Rejewsky. Knowing that the 1st and 4th letter in the encrypted message key (here A and U) is the encryption of the same letter (here E), he was able to set up mathematical relations. The same with the 2nd and 5th and 3rd and 6th letter in the encrypted message key. All this will be explained in closer detail in section 6 and especially in the article in section 7.
Another difference is that only 6 plugs were being used in the plugboard settings before the war, instead of the 10 plugs being used later! Using 10 plugs instead of 6 increased the number of combinations with a factor of more than a 1000.
The Germans also changed the procedure regarding the indicator setting. Before the 15th of September 1938 the Germans included the indicator setting in the daily keys in the monthy list. So it was the same for all messages sent for a whole day. In the above description the indicator setting was chosen by the operator himself for every new message!
As you can sense things changed over time and got more difficult, and inevitably it became too big a job for the clever guys in Poland to deal with. But before so the brilliant discoveries and experiences of the Poles were handed over to the British Intelligence. The story continues at Bletchley Park, where the resources and set up was much bigger!
Let's finish this section with a picture of a situation from World War II, showing how Enigma was in fact being handled in the middle of the battlefield:
|
|
|
The German General Heinz Guderian in a command-post vehicle. An Enigma machine in use! Copyright. The Art Archive. |
In this section I will give an outline of the mathematics used by the Poles in order to break Enigma. It will only be an outline, because I want interested students to be able to investigate the mathematics by working out details themselves. The interested reader should consult the next section.
What Enigma does is basically to substitute a letter with another one, so it should come as no surprise to the reader that it is the theory of permutations, which is the central mathematical subject involved. Enigma has 26 letters from a to z, so we are dealing with permutations of these 26 letters. One way to describe a permutation is to use two-row-notation, in which each letter in the bottom row is the image of the letter written directly above. As an example we can take the rotor I, of which the internal wiring is being described by the permutation:
![]()
Meaning that a map to e, b maps to k, etc. Another way of viewing the same permutation is to focus on images of images. Since the set is finite, it is always true, that after a while one will always end up with the starting element. A sequence generated in this way is called a cycle. The cycle starting with an a looks:
![]()
To find the rest of the cycles, continue with the first letter not present in the cycles already found: Here it is b, and we get the following cycle:
![]()
Continue this way and you end up with the so-called cycle-notation of the permutation:
![]()
The combination of cyclelengths (here 10 - 4 - 4 - 3 - 2 - 2 - 1) is referred to as the cyclestructure of that permutation. Later we will need the permutation P, which shifts all letters by one:
![]()
a maps to b, b maps to c, etc. Another important aspect of the theory of permutations is that a composition can be defined between any two permutations A and B. The composition AB is defined as the permutation, which results from first applying A, then B. Let's look at an arbitrary example:

It works in the following way: A maps a to d, B maps d to w, so AB maps a to w. Now we continue with w: A maps w to o, B maps o to l, so AB maps w to l, etc., etc. It should be stressed that I have decided to follow Chris Christensen and Marian Rejewski in their choice to let compositions take place from left to right, that is, when writing AB then A is understood to be applied before B. There doesn’t seem to be any convention in mathematics in favour of one way or the other. Some people prefer to let compositions take place from right towards left, as is the case with functions and matrices.
Another important definition is the concept of an inverse permutation defined as the permutation which cancel the effect of the original permutation, that is, if we apply a permutation and then the inverse (or in reverse order), we get the identity permutation I which does nothing and therefore consists entirely of 1-cycles, one for each letter. Obviously the inverse permutation can be achieved by simply reversing the direction of the cycles. For example:
![]()
Assume that A is the permutation corresponding to the internal wiring of some Enigma wheel with certain ring and rotor settings. Consider the following composition including the permutation mentioned above:
![]()
We will state without proof that this permutation actually represents the action of the wheel being advanced one step, before the signal is going through the internal wiring! In mathematics an expression of the form TAT-1 for any two permutations T and A is called the conjugate permutation of A by T.
A mathematical theorem - not very difficult to prove - states that the cyclestructure of a permutation is preserved under conjugation. This fact was one of the central points in Marian Rejewskis success in breaking Enigma. It will take us too afar to explain this in detail here. You can read about it in the article of Chris Christensen in the next section! However it should be mentioned briefly that the introduction of the plugboard to increase the number of combinations - and to which the security of Enigma heavily relied - did not change the cyclestructure of the permutation!!! Therefore Rejewski could decrease the work of finding the daily key dramatically, by working out a table of cyclestructures. It was still a very big task, and Rejewski used a number of ingenious tricks. But this mathematical analysis meant that the breaking of Enigma was within reach.
Let's conclude this section by looking at what happens when a signal goes through the entire Enigma circuit in terms of the permutations associated with every single step in the path through the circuit. First the signal goes to the plugboard represented by the permutation S, continuing until the three rotors, whose wirings give rise to the permutations N, M and L. Remember that already when pressing a key on the keyboard, the first rotor is being forwarded one step. According to the above comments, this means conjugation with P. After passage of the first rotor, the signal is permuted in the next couple of rotors, through the permutations M and L. Notice, that we here assume that the notch on the first wheel does not activate the next wheels! Marian Rejewski made the same assumptions. Of course once in a while the wheels do turn one step due to a notch activating the next wheel, and in those circumstances the below expression for the permutation doesn't hold. Now, in the reflector a permutation is taking place again, this time a so-called transposition, i.e. a permutation consisting of 2-cycles alone. The signal continues back through the rotors, but now in reverse direction and therefore the permutations are inverted! Finally the plugboard is reached again, this time also in reversed direction! Altogether we get the following composition for the first key press:
![]()
In the following we will look at the permutations associated with a true Enigma machine with wheel II as the first right) wheel, wheel III as the second (middle wheel) and wheel I as the last (left) wheel. Notice that the Germans used a number of different wheels introduced at different times in the War and before it. The wheels I, II and III were introduced in 1930 as can be seen in Wikipedia:
http://en.wikipedia.org/wiki/Enigma_rotor_details
In Wikipedia the permutations are given in two-row notation with the upper (obvious) row deleted! In cycle-notation the permutations representing the first three rotors are given by:
|
Rotor |
Date |
Permutation with default settings (ring setting A-01 and rotor setting A) |
|
I |
1930 |
|
|
II |
1930 |
|
|
III |
1930 |
As reflector we are using the reflector B. In this example we assume that all wheels have "default settings", i.e. ring settings are A-01 and rotor settings are A.

Notice that the permutations S and it's inverse are not complete. Each letter not presented are assumed to be mapped into itself, so the rest of the letters would have been 1-cycles, if listed! If you run through the above sequence of permutations you will realize a is mapped into e:
![]()
Try the Enigma simulator mentioned below and you will get the same result - with the "default settings"! If you are using different settings for the wheels, for example the middle wheel having the initial rotor setting f (5 steps from the letter a), the permutation M is changed. If R3 is denoting the permutation for the third (middle) Wheel having default settings, then M is given by the conjugation:
![]()
In the same way changing the ring setting from A-01 to B-02 amounts to the same as changing the rotor setting from a to z (one step backward) - besides one fact: The notch has been moved relative to the internal wiring! Let's stop the discussion of the mathematics here.
I am very happy to be able to bring an excellent mathematical account of the mathematics used by the Poles in order to be able to break Enigma shortly before World War II.
|
Chris Christensen. Polish Mathematicians Finding Patterns in Enigma Messages. Mathematics Magazine, Vol 80, No. 4, October 2007, page 247-273 (The Mathematical Association of America). |
Big thanks goes to the author Chris Christensen and Ivars Peterson from MAA for having allowed me to bring this article on my website. Chris is an expert in Cryptology after having studied it for many years. He has also drawn my attention on other important aspects of the story about Enigma. The Mathematical Association of America do publish several interesting journals, and subscriptions can be made online at www.maa.org .
It's my hope that students in late high school or college will be able to understand important parts of it. To make the article more accessible to those people, I have written a kind of guide document, bringing in the mathematical notion of a permutation etc. Also the document is built up on a number of exercises, so that students more or less will be forced to make their own contributions, that way not destroying the subject as a written exercise at school.
 |
 |
|
Polish Mathematicians Finding Patterns in Enigma Messages (861 kB) |
|
|
The mathematics behind the solution of Enigma (a guiding document)
(165 kB) |
Shortly before the World War II started the Germans changed habits regarding Enigma. In December 1938 two new wheels were introduced and the Germans also began using 10 plugs in the plugboard instead of the usual 6 plugs. This meant a lot of extra possible combinations. At that moment the work required to solve Enigma exceeded the capacity of the Poles at Biuro Szyfrów. A bigger set-up was needed. The 30rd of June 1939 the chief of the Polish cipher bureau, Langer, telegraphed his French and British counterparts, inviting them to Warsaw for a talk about Enigma. The meeting tool place on the 24th of July. The French and British Intelligence representatives were both very astonished to realize that the Poles had been able to break Enigma for years. In particular the Frenchmen were surprised, since they had earlier handed over important information about Enigma to the Poles - they believed Enigma to be unbreakable. The English and the French were each offered a replica and a blueprint for the Polish bombs. The two Enigma machines were secretly smuggled to Paris and over the Channel to London.
Traditionally the British cryptography office named Room 40 had been occupied by linguistics and classic scholars, crosswords addicts and the like. Now inspired by the Poles, they also engaged mathematicians and scientists. However, they were not sent to Room 40 in London, but to Bletchley Park, The Government Code and Cypher School (GC&CS), situated at Milton Keynes, about 50 miles north west of London. Here there were plenty of room for expansion. The director of GC & CS was Commander Alastair Denniston. Soon several simple wooden huts were erected to house some of the many code breakers, who would soon join at Bletchley Park. In his "The Hut 6 Story" Gordon Welchman explains how he recruited friends and former students. One of them was Stuart Milner Barry from Trinity College, who was a brilliant chess player, having played for England. Welchman himself had been a lecturer in mathematics at Cambridge since 1929 (Algebraic Topology). BP were in particular looking for "Professor type people". Lots of young people were recruited many from neighbouring Oxford and Cambridge, but also London Banks were sending their brightest young men to handle the interchange of information with intercept stations. Also Naval and Army staff was required for the Intelligence sections. Around 3/4 of all people employed at Bletchley Park were in fact women. One group of female participants were the so-called Wrens (or WRNS for Women's Royal Naval Service). They included cooks, clerks, wireless telegraph operators and electricians. Many women were used to operate the so-called bombs.
The big hero at Bletchley Park was Alan Turing (1912-1954). He was a mathematical genius from Kings College, Cambridge. Not even 24 years of age, in 1936, he submitted a groundbreaking article "On Computable Numbers with an Application to the Entscheidungsproblem", a highly abstract subject within the area of Mathematical Logic. His article gave rise to the notion of a Turing-machine, now a central object in the Theory of Computation. It can be argued that he actually
was dealing with problems of a computer, before the computer was even invented. Therefore he could be considered the right man on the right place at the right time, when the War started and England needed his insight! But a theorist does not always make a practical person. However Turing proved his ability in this respect too, describing the design of a machine, which could check a lot of different Enigma settings in a very short time. This machine was called a Bomb, a name adopted from the Poles, who
used the
name to denote another machine to crack Enigma. Gordon Welchman, however, made a very important contribution to the design of the bomb by inventing what was is now called a diagonal-board.
|
|
|
Alan Turing on election to Fellowship of the Royal Society, 1951. Copyright. The Art Archive. |
Before we continue giving more information about Blechley Park, lets look at the way messages were being handled there.
The decryption procedure at Bletchley Park is best described using a figure. First
 |
|
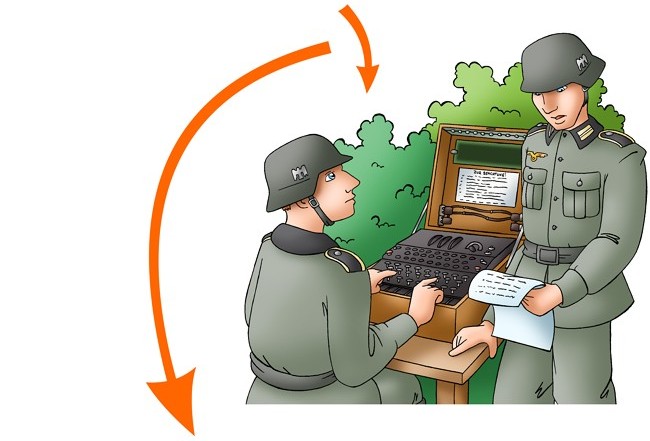 |
|
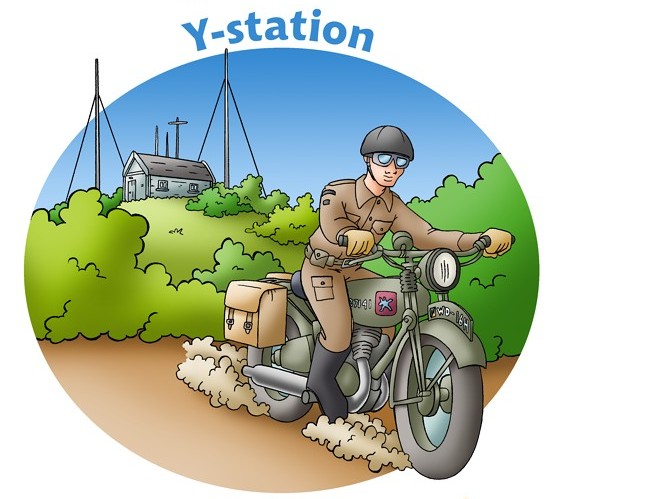 |
|
 |
|
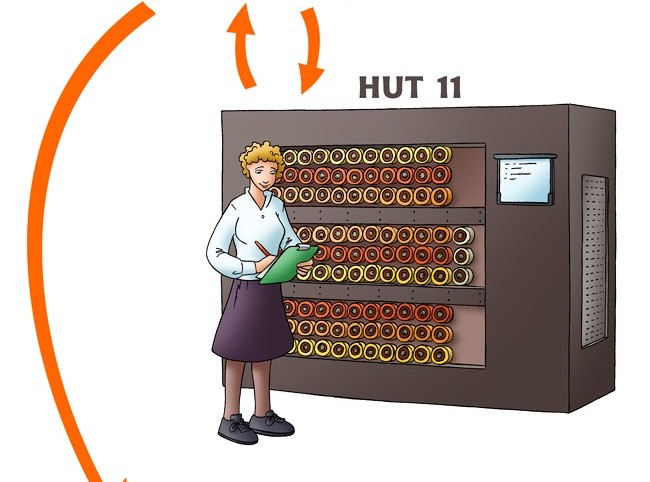 |
|
 |
Illustration: Jakob Kramer
As explained above, the people of hut 6 and hut 8 worked with the hardcore cryptanalytic problems. Usually they suspected a certain piece of plaintext to appear in the message. One good example is the German word Wettervorhersage, meaning weather forecast in English. For obvious reasons the weather often played an important role in the preparation of battles, so it is not a surprise it would often appear as part of the plain text. Such a piece of plain text, called a crib, was the first vital step in breaking the daily key. The people at Bletchley Park were very much aware of stereotypes used by the Germans, also by single persons. For example an officer in the Africa Corps helped a lot by constantly including the phrase "Nothing to report" in his messages. Sometimes when lacking cribs at BP, they made Royal Air Force deliberately send out false statements for example that the British had placed mines in a specific named area. With high probability the Germans would shortly after send out messages with the name of the area and the like. This was known as gardening.
The next step in the process was to compare the crib to the encrypted text: What part of the encrypted message was the encryption of the crib? Here a weakness of Enigma was exploited: A letter cannot be encrypted into itself! In the example below, the word "wettervorhersage" is placed under the encrypted text. The assumption that "pegmuoxyqwtjabx" could be the encryption of "wettervorhersage" can be ruled out, because it would mean that the second letter e is
enciphered into itself, which is impossible. Next, the crib could be shifted one place towards the right. This time apparently no contradiction happens. It is possible that we have a match between the crib and the enciphered text, but it is not certain. Many different methods and inventive ideas were being used in order to find a match. It was known that the Germans wrote numbers out in words, and Alan Turing reviewed decrypted messages and found that 90% of all messages contained the sequence eins for
the number
1. He then constructed an "Eins catalog". I won't go deeper into more details here.

When a possible plain text and matching encrypted text had been worked out, it was time for verification and if the match was correct, to find the daily key, in order for the whole document to be decrypted. Every plain text - encrypted text combination give rise to a so-called menu. We will be investigating this concept in the next section. Before we do so, I will show a couple of photos from Bletchley Park, shot during the War. I am grateful to Bletchley Park Trust for letting me display these photos
on my non-commercial site.
|
Girls from hut 6. Copyright Bletchley Park Trust. |
|
The hut 6 "machine room". Copyright Bletchley Park Trust. |
One of the really great accomplishments of Alan Turing was the fact that he - with his logical and mathematical mind - was able to invent an electro-mechanical device to check out a lot of possible settings for the Enigma machine in a rush! The nickname of his machine is probably inspired by the Poles, who called their machine, which was quite different by the way, bomba kryptologiczna. Loosely speaking the idea behind the Turing Bombe is to make an initial assumption, draw logical deductions, and prove that it yields a contradiction. The assumption is that some specific rotor orders and rotor settings are correct. We then try to solve the problem with the plugboard settings (stecker connections). If there is no solution, the assumption must be wrong. This is how Gordon Welchman expresses the idea of the Bombe in his Hut 6 story (page 239). Some books try to explain how exactly the Turing bombe worked. Often they are hard to understand, because they leave out important details. I have, however, found a very good account on this issue at www.ellsbury.com. Part of the following is inspired by his approach.
Firstly Alan Turing recognized that in order to use the enigma machines in a circuit it was necessary to make them "double-ended". Instead of the signal going through the plugboard, the rotors and the reflector and back again, Turing designed a double-ended Enigma. The effect of going through an ordinary Enigma and a doube ended version is the same.
|
Figure 1 |
|
The middle part of the double-ended Enigma machine we will denote as the Double scrambler. In the following the double scrambler will be depicted as a single figure:
|
Figure 2 |
|
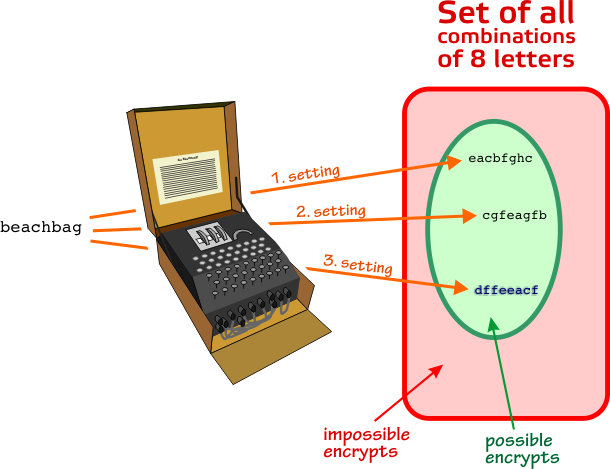
Next we need to consider the menu, which contain the match between the plain text crib and the encrypted text, as described in the previous section. To keep figures sufficiently simple, I will assume in the following that we are dealing with an alphabet of 8 letters. I will assume that hut 6 has created the following plain text - encrypted text match:
|
Figure 3 |
|
First b is enciphered into d with the rotors in a position, which we will refer to with the label 1, then e is enciphered into f with the rotors in the next rotor settings labelled 2, etc. The situation can visually be illustrated in a menu like this:
|
Figure 4 |
It should be emphasized that inherent in the situation are strong conditions for this encipherment being possible. This is best visualized by putting in position in the diagram the double scramblers with plugboards. The double scramblers are labelled 1, 2, etc, according to the order in which they are being applied: The rotor settings of double scrambler 2 are those you get when pressing a key after the rotors being in a position described by doublescrambler 1, etc.
|
Figure 5 |
Now, it is important to note the set-up: We assume that some three specific rotors being used and put in a specific order (see rotor arrangements) , we assume a specific reflector being used and in addition we assume the rotors in double scrambler 1 having some specific rotor settings, say e, c and e for the left, middle and right rotor respectively. Then the settings of the other double scramblers are uniquely determined. With those very specific
assumptions we could ask ourselves: Does there exist any plugboard settings, which would make the plain text "beachbag" being encrypted into "dffeeacf"? The straightforward way to answer that question would be to simply try every single possible plugboard setting. Because there are more than 100 billion combinations depending on how many plugs being used, this would take years ... Another and more powerful method was needed. It was here that Alan Turing discovered a pattern. Let's assume in
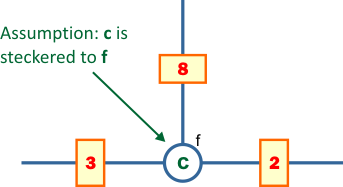
the above
diagram that there is a plug connecting the letters f and c in the plugboard. We also say that f is steckered to c (the plugboard was also called a steckerboard). We can then put the letter c in the three positions connecting to the letter f in the above menu.
|
Figure 6 |
We are now able to make deductions. Because we know the settings of the double scramblers 2 and 3, we can find the encipherment of c in both of those double scramblers. They turn out to be d and e respectively. The letters can be put into the diagram. We realize that our assumptions means that a is steckered to e and e is steckered to d. Already here we see a contradiction, because a letter cannot be steckered to more than one letter (e can't be steckered to both a and d)! A contradiction could also have been discovered by making more deductions as have been done in the diagram: Because e is steckered to d, we can continue down the angled path to the letter c and finally we return to the letter a. Contradictions are often revealed when taking a tour around a loop in a menu, but it can also be determined in other ways. As indicated in the figure we get the contradiction that a is steckered to both e and h! So even if our crib is correct, we can conclude that the plugboard assumption of f being steckered to c is wrong!
The straightforward method would then be to try a new plugboard assumption. Alan Turing, however, noticed that in the above deductions the plugboard settings are not being used at all, only the double scramblers and how they are interconnected. This means that we can "contract" the above menu-diagram to the following:
|
Figure 7 |
As above, c is assumed steckered to f, hence placed in the f-circle. In accordance with our above deductions, we can write the letter d in the e-circle, the letter g in the c-circle and both the letter e and h in the a-circle. The latter is a contradiction ... Alan Turing noticed that "shooting" though the circuit described by the menu, back and forth, you get all kinds of false stecker combinations, so it is usually possible to rule out every plugboard setting in one run!!! This was the big clue. So if for example we are assuming f is steckered to c and in the run through the circuit deductions are made that f must also be steckered to b, d, e, f, g and h as well, we can rule out everything at once! Here it turns out that there is only one missing, namely the letter a. I will get back to this a little later.
Of course Alan Turing realized that all those deductions could not be made by hand. The work required was immense! So he went on to design a machine, the Turing Bombe, to do all these tests automatically. The result was a big machine constructed by the British Tabulating Machine Company at Letchworth under the competent direction of Harold "Doc" Keen. The codename of the machine was CANTAB. The Bombe was about 7 feet wide, 6 feet and 6 inches tall and 2 feet deep. It consisted of a lot of wires and cables and drums. I won't get too much into the technical details just explain the idea behind it by showing a wiring diagram. I hope the reader will appreciate the construction, remembering the limited technology at hand at that time. With todays computer it would have been a simple matter to make a program doing the tests. During World War II the options were to use electric circuits and valves!
In the following illustration I have adopted the style used by Graham Ellsbury to illustrate how the Bombe is wired, used on my own example. I am grateful to Ellsbury for the permission to use the same diagramming, which is copyright, and strictly forbidden without a written consent of the copyright holder. The actual page can be found at www.ellsbury.com/bombe3.htm . This page helped me understanding the
idea behind the Alan Turing Bombe during WWII. You can find a lot of other useful material on his general page www.ellsbury.com.
Figure 8
The Turing Bombe had one cable for every letter in the alphabet, that is 26 cables, and every cable consisted of 26 wires. My reduced model has only 8 cables, one for each of the eight letters in "my alphabet". Remark the ingenious construction in the upper part of the figure. It is called the Diagonal Board and connects wire b in cable A to wire a in cable B, wire c in cable A to wire a in cable C, etc. This part of the Turing machine was a very clever and very important addition to the original design of Alan Turing. This construction was due to another mathematician, Gordon Welchman, head of Hut 6. The diagonal board reflects the obvious fact that if a is steckered to b, then b is steckered to a! This contribution by Welchman explains why the Turing Bombe is sometimes referred to as the Turing-Welchman Bombe.
Let me explain the situation in the above figure. The double scrambler 1, which has rotor settings e, c and e. is placed between cables B and D, in accordance with the menu. Remark that the settings of the rotors in double scrambler 2 are e, c and f, obviously reflecting the fact that the right rotor has been forwarded by one step! Similarly conclusions for the other double scramblers. Now we are ready to "shoot" through the circuit. The first thing is to place a test register on one of the cables. Usually the cable chosen are the one representing the letter occurring the most frequently in the menu! Here it is the letter f. Let's say that we send a signal through the c wire in the f cable. Immediately the current runs through the double scramblers and the wires. In this case almost all wires are made "live", shown by black wires. Only the wires illustrated with a yellow color are not reached. The conclusion is that f is NOT steckered to c, because the implications are, that then f should be steckered to all the wires b, d, e, f, g and h too, which is impossible. The reason why a is not reached is that f is in fact steckered to a! And the crib is correct. Let's see what happens if we had been shooting through the a wire in the f cable instead of the c wire:
We notice what happens when the true settings are made and the correct match between plain text and encrypted text has been made (that is: The crib is correct): Then at most one wire in each cable is brought to life! Now the reader might ask what will happen if the initial assumption with the crib is false? In the vast majority of cases using the bombe all wires in the testregister will be brought to life. These facts suggest a useful stopping strategy to depend on the number of wires in the testregister being brought to life. If the crib is correct and the rotor settings are correct as well, then it will normally happen that either exactly 1 wire or eaxctly 25 cables are brought to life in the testregister, dependent on if the steckerassumption made is correct or false. In both situations we want to stop the Bombe because we are on the right track. Sometimes however, the current won't be able to reach all 25 wires mentioned in the latter case, maybe because the menu is too short or their are not sufficient loops. Therefore one need to make the stop-strategy sound: If there are fewer than 26 cables alive in the testregister, the Bombe should stop. After a stop it is then necessary to investigate further if the stop is a true stop or a false stop. I won't describe the procedures applied in that situation. It is quite complicated and the interested reader is encouraged to read the following webpage written by Frank Carter:
Here it is explained how the "expected" number of false stops is highly dependent on the number of letters in the crip and how many loops it contains. Alan Turing carried out some extensive statistical calculations to be able to give an estimate of this dependence.
The above test was made under the assumption of some specific rotor settings. If the actual settings were not provoking a stop - in which case either the crib was false or the rotor settings were false - the Turing Bombe would automatically turn the right rotor one step in the double scramblers. 120 settings could be tested in one minute! You might wonder why the Bombe did not need to test the different ring settings. Had this been necessary the time required to do the testings would have been multiplied by a factor of 676 (which is the number of different ringsettings) making the Bombe virtually useless. Fortunately changing the ringsettings amounts to the same as changing the rotor settings, except that the notch is being moved relative to the wiring! This fact has been explained in the last part of section 6. So if no turnover occurs, changing the rotorsetting would have the same effect. I won't go into the additional complication caused by a possible turnover of the middle wheel, just refer to the above document by Frank Carter.
Then there are the rotors and rotor orders! In much of the Army Traffic for example three wheels had to be picked out of 5 possible wheels, making 10 possible choices. And these three wheels could be placed in 6 different orders, making it 60 possible rotor/rotor order combinations. Each of these had to be tested in the above way. Often many Bombes were being employed simultaneously.
Let's finish this section with a summary of the idea behind the Turing Bombe and make some conclusions. It might be helpful in understanding the above theory better. I will be referring to the figures above through their numbering.
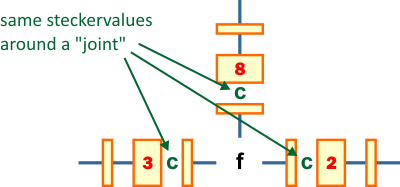
|
In Bletchley Park they have constructed a replica of the Turing Bombe. |
Let me finish this section by offering to the reader a couple of Microsoft Excel files. I have used Excel VBA to create simulation programs for the Enigma machine as well as the Turing Bombe. There is a help page inside the Excel file.
|
Enigma simulator in Excel VBA (101 kB) |
|
Turing Bombe simulator in Excel VBA (210 kB) |
NB! The Excel files will only work, if you accept the macros when opening it! I certainly don't expect any problems using these files, but of course I need to make the usual reservations: In no event shall I be held reliable for any damages or losses incurred either directly or indirectly in relation to the use of the files. The code only works in Windows, because the underlying programming language is Microsoft's Visual Basic!
Below I tested the Excel Turing Bombe on the situation with the Mini Enigma, described above. The menu is "beachbag" (Plain text) and "dffeeacf" (Encrypted text). For the rotors L, M and N the notches are fhc, ring settings aaa, rotor settings at start is ecd. Test register cable is f, test register wire is c. The permutations associated with the three rotors and the reflector is hcfagbed (R1), acgbhedf (R2), efchgbda (R3) and egdcahbf (Reflector) in two-row notation without the upper row. If you press the One step button, you will currently see which wires get alive for each passage of the double scramblers, or, if you press the Complete button you will see the process go all the way to the end. We see the results are in agreement with the wiring diagrams above.
Finally one realistic example below. Here I am using my Turing Bombe Excel simulator with the historic rotor I as the left rotor, rotor III as the middle rotor and rotor II as the right rotor. As reflector I use the wide B reflector. Ringsettings aaa, rotor settings sfd. The menu is "wettervorhersage" (plain text) and "aaqoanlnycxkvspx" (Encrypted text). The test register is applied to cable a. Shooting in wire p yields the below results, indicating it is the wrong wire, but that the menu is correct. (The Complete button has been applied).

The code breakers at Bletchley Park used a multitude of different tricks to break Enigma. In the case of the Navy's three-wheel Enigma machine (Kriegsmarine Enigma) M3, Alan Turing introduced statistical methods to ease the work of breaking the code. In 1939, the M3 variant of the Enigma machine had three extra wheels added, so that now 3 wheels had to be chosen out of 8 possible wheels. In the army's Enigma machine (Wehrmacht Enigma), as described in section 5, only 3 out of 5 wheels had to be selected. This meant that the fleet's Enigmachine immediately became more difficult to break. Now suddenly there were 8 × 7 × 6 = 336 possible ways to choose wheels including placement. This meant that much more testing had to be done on the Bombe machines, cf. section 11. It could take several days before the code was broken! Here it was that Alan Turing's statistical methods came into their own, as you could often narrow down which wheels could be in the right and middle places. Sometimes you could reduce the number of possible wheel combinations including position all the way down to 20. Moreover, the Germans had chosen a somewhat different encryption procedure for the navy than the one they used for the army. The Navy's procedure involved both trigram and bigram codebooks. We will not go into details here.
The statistical methods are based on Bayes' formula. Overall, the success of the methods is based on the fact that the individual letters of the alphabet (here the German) do not occur with the same frequency in ordinary clear text. Statistical attacks have been seen further back in history. In a monoalphabetic system where each letter is replaced by another (substitution), one can with great probability assume that the letter that occurs most often is the encryption of an E, etc. Also a polyalphabetic system such as the Vigenére cipher can be attacked, namely by using the so-called Friedman test. In the Vigenère cipher a letter can be encrypted to more than one letter, which means that the letter frequencies will be smoothened out in the encrypted text, making it more difficult to break. The Major Friedrich Wilhelm Kasiski (1805 – 1881) and especially the cryptologist William F. Friedman (1891-1969) however succeeded in attacking such a system statistically as well. Friedman introduced the notion: Index of Coincidence. If the letter frequencies had all been the same (that is 1/26 for the English language), the attacks would fail. The same is the case with Alan Turing's statistical methods. The difference is just that Alan Turing extracts even more information from the present data or evidence (the encrypted text), making the method even stronger. This is also necessary because the Enigma encryption is more complex than the other cryptosystems mentioned. As said, Alan Turing indirectly used Bayes' formula involving conditional probabilities. Using this formula, he could assign "scores" to various elements of the ciphertexts and look for a setting that would give rise to the highest score. The setting in question would then be the most likely. This way it was possible to deduce what wheels would be the most probable on the right side and in the middle.
The procedure, which involved the mentioned statistical methods, was given the name Banburismus. This somewhat silly name is due to the fact that special sheets of paper were used in the process, which were produced in the English town of Banbury, located just under 50 km from Bletchley Park. A "score" was given in the unit deciban or half deciban. The name is inspired by decibels, known from physics in the theory of sound pressure, and by the town of Banbury. As is the case for decibels, decibans are also defined via a logarithm. The advantage here is that logarithms "turn multiplication into addition". Thereby one did not need to multiply numbers together manually, but could be content with adding numbers together manually in order to find the total score.
The work on Banburismus took place in Hut 8, where the best code breakers were located, including the chess master Hugh Alexander, I. J. Good, Joan Clarke and others. The first day Hut 8 succeeded in breaking the Enigma code for a day using Banburismus was in November 1940. The day was subsequently named "Foss's Day", in honor of Hugh Foss who was responsible for the breakthrough. From the beginning of 1941, they were able to break the navy's Enigma machine M3 regularly, and they did so into 1943, except for a period in 1942, when the Germans changed things, and intercepted code books from German ships were also missing. Gradually, the Germans also brought an Enigma M4 to the fleet, which made the job even more difficult for BP. Banburismus could not help break the M4. However, the people at BP also continuously improved their methods. Over time more Bombes were also received at BP so that tests could be carried out automatically.
Finally a few general words about how the procedure of Banburismus was carried out in practice at BP. It will be too difficult to describe the process in details. The goal was to find German messages, which could be "set in depth" as they called it at BP. Two messages can be set in depth, if there are parts of either message, which has been encrypted with the exact same Enigma settings as well as wheels being used and their position. In order to decide where two such messages might "overlap", the people from Hut 8 applied two sheets of paper from Banbury. The encrypted messages were "typed in" on the sheets containing pre-printed letters by making a hole in the sheet for the position of every letter in the message. Then the sheets were put on top of each other with a lamp underneath. By sliding one of the sheets along the other sheet it was easy to recognize repeats, that is identical letters and also bigrams, trigrams, etc. Simplifying it too much, one can say that the more repeats, the bigger probability that the messages were placed correctly in depth. It is however not quite the number of repeats, because bigrams and trigrams count especielly high - all dictated by the score in half decibans, which Alan Turing had calculated beforehand. One example is shown on the figure below, where an X is denoting a repeat-letter (painted red) and 0 is denoting different letters. We also discover a bigram and a hexagram. When Alan Turing created his scorings, he looked at the configuration of X's and 0's as divided into independent blocks - indicated by blue arrows (click for a bigger image):
In the same way BP found other pairs of messages in depth that day. Eventually it was possible to put the results into a "chain", making it possible to rule out the presence of some wheels. Interested readers can consult Wikipedia with the search word "Banburismus".
Below is shown a part of a Banbury sheet with printed letters. A message was "typed in" on the sheet by punching out holes in the sheet.
TedColes, CC BY-SA 4.0, via Wikimedia Commons. Lettere redigeret.
Thanks to the breaking of the Navy's Enigma, it was possible for large periods to direct Allied ships away from clusters of German U-boats, known as "Wolf-packs", which was of great importance in the "Battle for the Atlantic".
Since we cannot go deeper into the mathematics and especially the probability calculus that underlies Banburismus here, I have chosen to write another page about Turing's attack on the Vigenère cipher. This also involves using Bayes' formula. Interested readers can press the button below.
Let's return to our visit at Bletchley Park (BP). Only five minutes walk from Bletchley Railway Station and we were in front of Bletchley Park National Codes Centre. We were kindly received by Graham Hoare, who brought us to Block B, where we were given an interesting one hour talk about the history of Enigma and the role of Bletchley Park during the War. He also taught us a little mathematics while demonstrating a real Enigma machine. Afterwards we went for a guided walk in the beautiful Park.
|
A walk in the park |
After consuming a meal in a restaurant placed in one of the old wooden huts, housing the code breakers during the War, we continued our tour in the Park. On our way we passed the house where Turing had been working. He was known for being a kind of eccentric. In periods when suffering from hay fever he was riding a bike wearing a gas mask! Turing was an excellent marathon runner. His all time best of 2 hours 46 minutes and 3 seconds was only about 11 minutes slower than the winner in the 1948 Olympic Games.
|
Turing worked here from 1939 to 1940 until he moved to hut 8 |
|
A statue in honour of Alan Turing, here placed in Block B. |
It is a real sad story how Alan Turing ended his life. Sometime in 1952 he revealed to the Police, while reporting a burglary, that he was a homosexual. At that time in Great Britain being gay was considered a mental illness and subject to criminal sanctions. Turing was given the choice of imprisonment or probation with the condition that he would receive hormonal treatment. He accepted the latter. For one year he received oestrogen hormone injections. In addition he was not any longer used as a consultant for GCHQ (Government Communications Headquarters) on cryptographic matters - he was considered a security risk. Finally in 1954 he did commit suicide in a fit of depression.
Alan Turing is widely regarded as a very significant figure during World War II, and being one of the fathers of the modern computer. Today the A. M. Turing Award is being given annually to a person delivering important and lasting contributions of technical nature to the development of the computer - the "Nobel Prize" for computer people! Although he certainly did not receive the recognition he deserved while he was alive, partly because of the secrecy surrounding the whole operation at Bletchley Park during and after WWII, he did get in 1945 an OBE (Officer of the British Empire) award for his wartime contributions.
|
The characteristic main building at Bletchley Park, a rather ugly mix of architectures: Victorian Gothic, Tudor and Dutch Baroque. |
|
In Hut 6 the encrypted messages from the German Army and Airforce Enigma machines were being analyzed using cryptanalysis. Today this hut is in a rather bad shape. |
|
Hut 1 was the first building to be built. Today it is used to display a collection of Diplomatic Wireless equipment. |
On our way back to Block B, we got trough a building housing one of the other important machines, Colossus, which was used to break codes. This time it was the German cipher machine Lorenz SZ 40/42, originally constructed by Tommy Flowers back in 1943. It took him 11 month to finish this machine, which can be considered the first programmable machine ever. After the War all these machines were dismantled due to secrecy. In the 1990's a very dedicated man, Tony Sale, rebuilt it. Tony is a very kind man and happy to show the machine for anyone. He even gave me one valve from the rebuilt machine. It is displayed on a photo below. Our guided tour ended in a museum from the War, displaying different crypto machines and items from the War along with wall sheets with photos and information.
|
Tony Sale in front of his rebuild of Colossus |
|
|
|
A valve from the rebuilt of Colossus |
At the entrance to Kiel Fjord in Germany is a resort named Laboe. Here is a place called Laboe Naval Memorial. I had the pleasure of visiting this site in 2023. In addition to an 85 meter high tower commemorating people of all nationalities who died at sea, the Laboe resort also houses a famous German submarine U-995. It is a submarine of the type VII C (Baureihe VIIc/41). The Type VII was the most common German submarine type, and until 1944 a total of 663 submarines of this type were built. With a length of 67.23 meter and a width of 6.20 meter, it is a medium-sized submarine. U-995 took part in the war, and is one of the few submarines that actually survived the war and the time immediately after. The submarine was built in 1943 at the Blohm & Foss shipyard in Hamburg and managed to be in action a total of 9 times. It was deployed as part of a German submarine fleet in Trondheim, in occupied Norway. Operating from Norwegian ports, U-995 was deployed against Allied convoys in 1944. In that connection, it sank 2 merchant ships, a Soviet escort ship, a Soviet minesweeper and a Soviet motorboat. After the German capitulation, England took over the submarine, and in 1948 it was handed over to Norway. The Norwegians gave the submarine a new name and used the submarine to train Norwegian submarine crews. When the submarine was decommissioned in 1962, the submarine was offered to the Bundesrepublik Deutschland as a sign of reconciliation - under the condition that the submarine in a dignified way would be made available to the public as a technical museum. After long negotiations, the German Marine Federation (Deutsche Marinebund) declared itself ready to place the submarine at Laboe. After repairs and conversions, the submarine was finally placed in its current location on the 13th of March 1972.
The pictures below is showing the U-boat U-995 (click for a bigger image).
Inside the submarine, you can feel the cramped space the crew had to live under. And the air in the submarine was not fresh either. There was a mixture of diesel smell and body odor. Below the room with diesel engines.
At the front of the submarine there are four torpedo tubes for the 7.16 meter long and 0.533 meter wide torpedoes, which in water could move forward with a speed of approximately 55 km/h.
and various instruments:
The submarine has a radio room (Funkraum) as well as a listening room (Horchraum). In the former one could receive messages or orders via radio signals directly from other submarines or from Admiral Karl Dônitz, who was the Commander-in-Chief of the German Navy, Kriegsmarine. Radio communication was however reduced to the most necessary, because radio signals could be intercepted by the Allied, thereby eventuelly put the U-boat in danger. The listening room, also called "hydrophone rooms" played a crucial role in detecting and tracking enemy ships, particularly during underwater operations. Hydrophones, which were underwater microphones, were installed on the U-boat's hull and connected to the listening room. The U-boat crew would use the listening room to detect and avoid enemy ships while remaining submerged.
Below a picture from the Radio Room of U-995 (click for a bigger picture):
By clicking the button above one can see the content of the radioroom. Maybe especially interesting is the fact that U-995 used the Enigma M4.
The German submarines were especially deployed in the North Atlantic to stop merchant ships from bringing supplies to England from Amerika. Twelve hours after England declared war on Germany, the British passenger liner ATHENIA was sunk by the German submarine U-30 (September 3, 1939). Out of 1,400 people, 112 perished, including several Americans. At this time, the Germans had 57 submarines, of which only 22 were deployed in the Atlantic. Although Germany did not have many U-boats at the beginning, they could do a lot of damage, while at this early stage they themselves did not suffer many losses. It only came later. The submarines often operated in packs, the so-called "wolf packs". Several submarines could coordinate their attacks via mutual communication. During 1941, the British succeeded in breaking the Germans' encrypted messages, which allowed convoys to avoid U-boat positions in order to reduce shipping losses. Countermeasures against submarines were also developed. The main reasons for the defeat of the Germans in the battle for the Atlantic were several: too small a number of German submarines, continuous improvement of convoy security, technological advancements (the development of advanced anti-submarine weapons, such as depth charges and sonar) and the decryption of the German messages was very important along with air surveillance and the use of radar. Also the construction of new ships in America outnumbered the losses in the Atlantic. That way the Germans never succeeded in isolating England.
Many of the German men on the submarines were very young. The average age was 21 years. Many volunteered, lured among other things by the war propaganda that made it appear heroic to be on the submarines. The crew felt like a kind of elite in the German war machine. However, the reality turned out to be very different to the false idealization delivered by the heavy German War propaganda. In addition to the hard life onboard the submarines, tens of thousands of German submariners had to pay with their lives in the Battle of the Atlantic and fights elsewhere.
A German submarine hero was Günther Prien. Under his command, the submarine U-47 sank over 30 ships with a total weight of approximately 200,000 gross register tonnes. He even succeeded in sinking the otherwise heavily protected British battleship HMS Royal Oak at Scapa Flow at the Orkney Islands. For this feat, he became an instant hero in Germany and was the first to receive the Knight's Cross of the Iron Cross with Oak Leaves (Ritterkreuz des Eisernen Kreuzes mit Eichenlaub). Prien did not return from a mission in March 1941 and on 24 May 1941 he was presumed dead. But his hero status lived on and the youth novel "Prien Greift an" was published for the first time, which was to become a bestseller. Also board games were published.
Another German U-boat hero was Otto Kretschmer. As the most successful, he was nicknamed "The Ace of Aces". He survived the war and died in 1998.
The picture above shows the top of a box containing a board game from 1941. The motive is painted by the maritime painter Adolf Bock.
There are several Enigma simulators out there on the Internet. I can warmly recommend the simulator of Dirk Rijmenants. He deserves high praise for his simulator, which can be downloaded from the following site:
https://www.ciphermachinesandcryptology.com/en/enigmasim.htm
The simulator is impressing in its layout - having a real touch and realistic feeling to it as indicated by the screenshots below. It is very customisable: You can open the cover of the machine, pick out which wheels to apply in the "engine room" of Enigma with a single click, adjust its ring settings and put it into place. The reflector can be selected and the "engine room" closed. Now you need to set the plugboard by connecting plugs using clicks. Finally you are supposed to make the rotor settings (ground settings) by clicking a number of times on the wheels when the cover is closed. Now you are ready to encrypt! Click on the letters on the keyboard. The encrypted letter is shown briefly on the lampboard. Afterwards you can watch the encrypted text by selecting clipboard when rolling over the text-rectangle in the upper right corner. The function of the simulator is explained in a 18 page manual ready for download. It is very intuitive and you will grasp the idea fast, trust me!

Other resources:
www.cryptomuseum.com (Here are links for different simulators for Enigma machines). http://www.simonsingh.net/The_Black_Chamber (Simon Singh has produced a "Black Chamber", where the user is invited to test a whole range of different ciphers employed during history).
www.bletchleypark.org.uk (The official page of Bletchley Park. You can arrange lectures there for school and high school students! Look here: https://bletchleypark.org.uk/learning/
www.turing.org.uk/sources/archive.html
www.ellsbury.com (A very good page, especially regarding the Turing Bombe).
www.codesandciphers.org.uk (Tony Sale is a very dedicated man. He has produced a copy of Colossus at Bletchley Park).
www.alanturing.net
www.ilord.com (Bob Lord's page is a very different and interesting one. Lot's of technical stuff about Enigma and other cryptograpic machines, scans of manuals, decrypts from Bletchley Park, War posters and articles from Life Magazine, etc.).
http://cryptocellar.org (Impressive page about Cryptology. Here you can get loads of information).
https://www.ciphermachinesandcryptology.com/ (Dirk Rijemenants' page about various crypto machines. An absolutely great page for readers interested in technique and simulators of historical machines).
http://uboat.net/technical/enigma_breaking.htm (A great page by Ralph Erskine - an expert on Uboats and Enigma)
https://enigma.virtualcolossus.co.uk/ (Virtual Enigma)
Below a number of videos. The first is an excellent video, which also include the use of Enigma and the impact it had in history.
How The Allies Hunted Down U-Boat Wolfpacks (War Stories)
Battle Stations Radar Documentary (History of Wars)
Scapa Flow Raid - Sinking of the HMS Royal Oak by U-Boat Ace Gunther Prien
Numberphile: 158,962,555,217,826,360,000 (Enigma Machine) (Om Enigma maskinen)
Numberphile: Flaw in the Enigma Code (om Enigma maskinens svaghed)
The following films are dealing with Enigma:
Director: Morten Tyldum with manusript by Graham Moore. Actors: Benedict Cumberbatch, Keira Knightley, Matthew Goode, Rory Kinnear, Allen Leech, Matthew Beard, Charles Dance, Mark Strong and more.
Director: Michael Apted. Actors: Dougray Scott, Kate Winslet, Saffron Borrows, Jeremy Northam, Nikolaj Coster-Waldau.

Director: Jonathan Mostow. Actors: Matthew McConaughey, Bill Paxton, Harvey Keitel, Jon Bon Jovi, David Keith.

| [1] |
Stephen Budiansky. Battle of Wits - The complete story of codebreaking in World War II. Viking, Penguin Group, 2000. |
| [2] |
Chris Christensen. Polish Mathematicians Finding Patterns in Enigma Messages. Mathematics Magazine, Vol 80, No. 4, October 2007, page 247-273 (Mathematics Association of America). |
| [3] |
David Khan. The Codebreakers - The Story of Secret Writing. Schribner 1996 (originally 1967). |
| [4] |
F. H. Hinsley, Alan Stripp (editors). Code Breakers - The inside Story of Bletchley Park. Oxford University Press, 1993. |
| [5] |
Andrew Hodges. Alan Turing: the enigma. Vintage, 1992 (originally 1983). |
| [6] |
David Leavitt. The Man Who Knew Too Much - Alan Turing and the Invention of the Computer. Phoenix, 2006. |
| [7] |
Michael Paterson. Voices of the Code Breakers - Personal accounts of the secret heroes of World War II. David & Charles, 2007. |
| [8] |
Hugh Sebag-Montefiore. ENIGMA - The Battle for the Code. John Wiley & Sons, Inc., 2000. |
| [9] |
Simon Singh. Kodebogen - Videnskaben om hemmelige budskaber fra oldtidens Ægypten til kvantekryptering. Gyldendal, 2001. |
| [10] |
Simon Singh. The Code Book - The Science of Secrecy from Ancient Egypt to Quatum Cryptography. Fourt Estate Limited, London 1999. |
| [11] |
Gordon Welchman. The Hut 6 Story - Breaking the Enigma Codes. M&M Baldwin 2005 (originally 1997). |
| [12] |
B. Jack Copeland (Editor). The Essential Turing - The ideas that gave birth to the computer age. Clarendon Press, Oxford, 2004. |
This webpage has been revised in August 2023.
|
|