NB! Download dokumentet til din harddisk ved at højreklikke på
billedet og vælge gem destination som ... (hvis Internet
Explorer benyttes).
|
Dokument
|
kl.
|
Beskrivelse
|
|

|
2-3g
|
Prebens drivhus
Preben er en handyman og ønsker at
fremstille sit eget drivhus med sit eget helt unikke design. I denne
autentiske opgave skal Preben have hjælp til at bestemme vinklerne
mellem vinduerne i drivhuset. Drivhuset er beskrevet ved opstalt
og plantegning og man skal anvende rumgeometri til at løse opgaven.
|
|

|
2-3g
|
Beregninger for en varmluftsballon
En varmluftsballon
tænkes sammensat ef et kuglesegment samt en keglestub. Beregninger
og brug af grafisk lommeregner til beregning af volumenet. Herefter
ønskes udledt en generel formel for volumenet af et kuglesegment
og en keglestub. I fysik på Haderslev Katedralskole har vi arbejdet
med varmluftsballoner: Se note.
|
|
|
2-3g
|
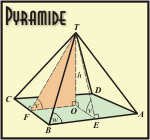
Pyramide udført i DMX plader
Kim er ansat i en virksomhed,
som fremstiller ovenlys vinduer og andre tagkonstruktioner. Pladerne
er 4cm tykke og skal skæres til i de rette vinkler. Du skal benytte
rumgeometri til at hjælpe ham. Opgaven er delvist autentisk.
|
|

|
1-2g
|
Model af halvkugle
I denne øvelse skal du forsøge
at konstruere en halvkugle i papir ved hjælp af en række strimler,
som forløber fra toppen mod bunden.Det springende punkt er
at bestemme formen på strimlerne. Hvis du har papir i stort format
kan du derefter fremstille halvkuglen i praksis og se, at beregningerne
stemmer.
|
|

|
1g
|
Vinkelmåling med sekstant
Virkemåden af en sekstant
undersøges: Man skal vise hvordan spejlanordningerne betyder at
man kan måle vinklen mellem objektstrålen og kimingsstrålen via
en speciel inddeling på sekstantens cirkelbue, kaldetlimben.
Hvis du er i besiddelse af fx en plastik-sekstant, kan du slutte
af med at bestemme højden af en mast.
|
|

|
3g
|
Vejgeometri
Vidste du, at man ved anlæggelse af veje
ofte bruger nogle meget specielle kurver, de såkaldte klotoider,
som er matematisk defineret, i linjeføringen? Eller vidste du,
at de selvsamme kurver benyttes i loops i forlystelsesparkernes
rutsjebaner? Du kan her downloade en større note om dette emne.
Noten på 42 sider med en stor opgavesektion kan måske benyttes i
3g matematik på højt niveau i et valgfrit forløb. Der er meget stof,
som kan være udgangspunkt for projektarbejde. Du kan læse mere om
emnet under emnet Vejgeometri.
|
 |
1hf, 1g |
Fitness matematik
Kostplaner og fitness er interessante emner i disse tider, hvor sundhed og velvære og ønsket om at fremstå med et mere perfekt ydre er vigtige for folk. I denne note ser vi, at man kan regne på ganske meget og eventuelt sammensætte en fornuftig kostplan til en selv. Desuden ser vi på betydningen af styrketræning og konditionstræning. Af matematik får vi brug for "høkerregning", procentregning, vejet gennemsnit, lineære modeller m.m.
|
|

|
2-3g,
2hf
|
Funktionsundersøgelser med Texas TI-89 Titanium
I disse CAS-tider er det tiden for en instruktion i brugen af TI-89, her specielt til funktionsunderøgelser. Noten indeholder en grundig instruktion og en lang række projektagtige opgaver. Desuden nogle opgaver med speciel udfordring.
|
|

|
1-2g
|
Isolering af ventilationsanlæg
Bo er en dansk pilot og en handyman. Et af hans projekter er at stå for ventilationen i eget hjem.. En af hans udfordringer er at finde ud af, hvordan isoleringsmaterialet til rørene skal skæres til, så det slutter pænt til. Det er ikke helt så simpelt, som denne opgave viser ... En god projektopgave!
|
 |
2-3g
|
Anvendelser af integralregning
Med indførelsen af integralregningen i 1600-tallet fik man et yderst kraftigt redskab til at løse praktiske problemer, fx i ingeniørvidenskaberne. I denne lille ikke-historiske note med opgaver skal vi se på, hvordan man gør i praksis. Først ser vi på et problem med at bestemme gennemsnitlige afstande på en øde ø, dernæst skal vi betragte tyngdepunktsbestemmelser for krumme flader, og der er opgaver til læseren.
|
 |
2-3g
|
Om bilers bremseevne
Med en simpel fysisk model kan man analysere bilers standselængde ved en given hastighed og beregne, hvor stor en afstand, man skal holde til en foranliggende bil. Mange undervurderer den nødvendige afstand for at være sikker på at kunne undgå sammenstød!
|
|

|
3g
|
En generel perspektivisk afbildning
De fleste bøger, som beskæftiger sig med perspektivet, koncentrerer sig om perspektivtegninger frembragt med lodret billedplan, hvilket er naturlig nok, da de fleste billeder og malerier er afbildet med et sådant. I andre tilfælde har man brug for at kunne afbilde perspektivisk på en hel generel plan, eventuelt med tiltet "kamera". Tænk for eksempel på, hvordan piloten i et fly oplever verden! I denne opgave skal du udlede en formel
for billedpunkterne ved en generel perspektivisk afbildning!
|
|
|
1-3g
|
Om at tegne en cirkel i perspektiv
Linjer afbildes i linjer ifølge de perspektiviske regler. Det er noget, som udnyttes kraftigt af tegnere. Kurver derimod, er noget mere komplicerede at tegne. I denne opgave skal du bevise rigtigheden af en lille genial konstruktionsmetode, hvorved man kan konstruere ekstra billedpunkter for en cirkel i perspektiv.
|
|

|
3g
|
Det skrå kast med luftmodstand
I fysikundervisningen er det skrå kast en fast bestanddel, i hvert fald i 3g, men her ser man normalt bort fra luftmodstand. Denne note, som omhandler tilfældet med luftmodstand, kan eventuelt danne udgangspunkt for et projekt i matematik og fysik eller for en studieretningsopgave. Dele af den er meget avanceret. Som tillæg kan du studere følgende Microsoft Excel fil, som simulerer det skrå kast med kvadratisk luftmodstand: Excel fil. Du skal tillade makroer for at kunne bruge filen, da den indeholder en del, som er programmeret i Excel VBA!
|
|

|
3g
|
Eulers metode
I fysikundervisningen er det skrå kast en fast bestanddel, i hvert fald i 3g, men her ser man normalt bort fra luftmodstand. Denne note, som omhandler tilfældet med luftmodstand kan eventuelt danne udgangspunkt for et projekt i matematik og fysik eller til en studieretningsopgave.
|
|

|
1g
|
Landmåling
Fra 1760'erne og frem til 1820 blev opmålinger til det første nøjagtige Danmarks kort gennemført. Den ledende person var den unge Thomas Bugge. Ved hjælp af et såkaldt målebord kunne gode lokale kort fremstilles. For at kunne sætte de mindre kort sammen til ét stort, foretog man desuden en triangulering af store dele af Danmark. I dette projekt lægger vi op til at læseren selv prøver at foretage en triangulering med et simpelt vinkelmålingsinstrument efter idé af Lars Thams. Derefter skal sinus- og cosinusrelationerne i spil, og man skal have passeren frem ...
|



