|
Det gyldne snit Det gyldne snit har i en lang årrække været populært at beskæftige sig med. Man hører det ofte omtalt og behandlet i kunstnerkredse, blandt andet af æstetiske årsager. Fascinationen af det gyldne snit skyldes også dets interessante historie, som er fyldt med mystik og symbolik. Nogle har omtalt det gyldne snit - også ofte omtalt som det gyldne forhold (Golden Ratio) - som værende et guddommeligt
tal/forhold.
Det er da heller ikke overraskende, at det er taget op i den Dan Browns klassiker Da Vinci Mysteriet (på engelsk The Da Vinchi Code). Men hvad er det gyldne snit egentligt, og hvad er årsagen til dets status i dag? Ja historien starter med grækerne, for hvem det var en kunst at konstruere tal med passer og lineal ...
1. En definitionLinjestykket AB siges at være delt i det gyldne snits forhold, såfremt delepunktet S er sat således, at de to stykker, som kommer ud af det, opfylder følgende: Hele stykket a+b forholder sig til det lange stykke a, som det lange stykke a til det korte stykke b. Dette forhold eller tal kaldes det gyldne snit og betegnes med det græske bogstav φ. Betingelsen er udtrykt som en matematisk ligning i den grønne ramme. Ligningen giver anledning til en andengradsligning,
som har to løsninger.
Den relevante løsning er den, som er større end 1. Løsningen er anført uden udledning i den orange ramme. Det er overladt til læseren som en opgave i min note nedenfor på siden at opstille 2. gradsligningen og løse den. Et naturligt spørgsmål er herefter, hvor stor en del det lange stykke udgør af det hele stykke. Svaret er:
2. Den græske matematik og naturfilosofiI det følgende vil jeg give en ret grundig præsentation af den relevante græske matematik fra oldtiden. Det kan måske virke mærkeligt at bruge så meget plads på det emne. Det er imidlertid efter min mening nødvendigt for at kunne forstå og værdsætte det gyldne snit og dets historie. Uden den græske naturfilosofi og forståelsen af den rolle de hele tal, deres forhold og geometrien spillede dengang og langt op i både middelalderen og renæssancen, vil det gyldne snit blot være et specielt tal med nogle smukke egenskaber, men uden de idéer, som ligger til grund for det, og uden en forståelse for de myter, som omgærer det. Den græske matematik, herunder især geometrien, har haft en markant indflydelse på matematikkens udvikling. Det var da også grækerne, som introducerede beviset. En af de første filosoffer og matematikere, der nævnes, er Thales fra Milet (624 f.Kr.-546 f.Kr.). Han er anerkendt som værende den første til at bryde med den hidtidige mytiske verdensopfattelse ved at forklare naturlige fænomener ved hjælp af teorier og hypoteser, en forløber til den moderne videnskab. Næsten alle filosoffer
indtil Sokrates
fulgte Thales tilgang med at søge at forklare naturen som udspringende af ét urstof eller princip. Thales mente dog fejlagtigt, at dette urstof var vand. Thales' fortjeneste er måske især at demonstrere, at man bør studere verden ved at undersøge og analysere dens bestanddele på en rational måde, fremfor at fremsætte myter. Thales leverede også bidrag til astronomien. Ifølge Herodot var han i stand til at forudsige solformørkelsen den 28. maj i år 585 f.Kr. Thales hævdes desuden
at være ophavsmand
til flere geometriske sætninger, herunder den om, at topvinkler er lige store og sætningen om, at to trekanter, som har to vinkler og én side parvis lige store, er kongruente. Det siges også, at han har givet et bevis for sætningen, der siger, at hvis A, B og C er tre punkter på en cirkel, og AC er en diagonal i cirklen, så vil vinklen ∠ABC være en ret vinkel (jf. figuren til højre herunder). På grund af sene kilder hersker der dog lidt tvivl om, hvem der er ophavsmand til sidstnævnte
sætning (Se Heath, [7]). Nogle tilskriver sætningen til Pythagoras/pythagoræerne.
Pythagoras og pythagoræerneI det 6. århundrede før Kristus foregik der en persisk ekspansion, hvilket truede de joniske kolonier i Lilleasien. Det bevirkede en udvandring mod det stor-græske område. I denne bølge var der også joniske filosoffer. Pythagoras (ca. 570 f.Kr.- ca. 495 f.Kr.) skal have udvandret fra øen Samos til den græske koloni Kroton i Syditalien. Der er tale om den Pythagoras, hvis sætning om siderne i en retvinklet trekant, er så kendt blandt elever i Folkeskolen.
Pythagoras skal have grundlagt en filosof-skole i Kroton. Mens man ved meget lidt om Pythagoras selv, så er det sikkert, at broderskabet, som omtales pythagoræerne, eksisterede, og at det i starten havde et tydeligt religiøst formål, nemlig menneskets renselse. Tanken var meget fjern fra den græske religion, men kan have været inspireret af den persiske religions stærke dualisme ([4]). Mens renselsen af legemet skete gennem askese (blandt andet vegetarisme), skulle sjælen "renses"
gennem
oplysning og undervisning. Sidstnævnte var inddelt i en offentlig belæring af tilhørere (akusmatikere) og en hemmelig uddannelse af en inderkreds (matematikere). Ifølge [4] kommer betegnelsen matematiker for et medlem af inderkredsen af verbet mantháno (at lære), hvoraf máthesis (undervisning) og máthema (det lærte). Den oprindelige betydning af ordet "matematik" er altså det pensum, som den pythagoræiske inderkreds havde lært. Først da det pythagoræiske samfund var ved at
gå i opløsning, begyndte broderskabets hemmeligheder at sive ud til omverdenen. Ifølge Archytas (ca. 400 f.Kr.) har pythagoræerne efterladt kundskab om stjernernes hastigheder, opgange og nedgange, om geometri, aritmetik og sfærik. Ikke mindst var der også musikken. Man anså musik for at have meget med de andre discipliner at gøre. Alt tyder på, at pythagoræerne både har beskæftiget sig med den rene matematik samt dens anvendelser, herunder også som værktøj til en naturbeskrivelse. Der eksisterede
dog sandsynligvis ikke nogen entydig bestemt pythagoræisk filosofi eller religiøst system.
Pythagoræernes matematikGrækerne havde et talsystem (10-talssystem), og de tillagde tallet 10 en særlig betydning. Blandt andet fremkommer tallet som en summen af de første fire naturlige tal: 10 = 1 + 2 + 3 + 4. Men det var også besværligt at håndtere brøker i grækernes talsystem. Måske var det derfor, at pythagoræerne koncenterede deres indsats om de hele tal. De lagde dermed grunden til det første matematiske emne, som blev studeret af rent intellektuelle grunde, løsrevet fra den praktiske regnekunst. Senere samlede og systematiserede Euklid teorien om hele tal i hans store bogværk, ofte kaldet Euklids Elementer (se senere). Her blev blandt andet behandlet lige og ulige tal, primtal, sammensatte tal, indbyrdes primiske tal, kvadrattal, fuldkomne tal, etc. Udover talteori tilskrives Pythagoræerne også en lang række resultater indenfor geometrien. Den nyplatoniske filosof Proklos (412 f.Kr.-485 f.Kr.) beskrev senere pythagoræernes indsats derved, at pythagoræerne gjorde geometrien til en fri kunst. Derved mente han, at man gennem intellektuel og ren abstrakt tænkning søgte efter geometriens endegyldige idéer, løsrevet fra sanseerfaringer og anvendelser. Det er klart, at det kun var en lille inderkreds af matematikere, som kunne være med her. Pythagoræerne skal også have opdaget de inkommensurable størrelser, altså de tal, vi i dag kalder for irrationale tal - tal som ikke er forholdet mellem to hele tal. En legende fortæller, at opdagelsen skabte så stor et chok og usikkerhed, at det blev forbudt den indre cirkel af pythagoræerne at tale om opdagelsen til omverdenen. Da én af dem alligevel gjorde det, skal vedkommende have lidt skibbrud.
Et regulært polyeder kan defineres på lidt forskellig vis, fordi det har så mange smukke egenskaber. En mulig definition er: Et polyeder siges at være regulært, såfremt alle sidefladerne er ligedannede regulære polygoner og alle hjørner ligger på den samme (omskrevne) kugle. Med betegnelsen en regulær polygon mener vi en polygon, hvis sider alle er lige store og hvor alle hjørner ligger på den samme (omskrevne) cirkel. Der findes kun fem forskellige regulære polyedre. Navnene på disse er: Tetraederet (med 4 ligesidede trekanter som sideflader), Oktaederet (med 8 ligesidede trekanter som sideflader), Terningen (med 6 kvadrater som sideflader), Ikosaederet (med 20 ligesidede trekanter som sideflader) og Dodekaederet (med 12 regulære femkanter som sideflader).
De fem regulære polyedre, også betegnet de platoniske legemer (efter den senere græske filosof Platon) kendte pythagoræerne også til. Det er desuden sandsynligt, at de var i stand til at konstruere dem. Det implicerer også konstruktionen af en regulær femkant. Konstruktionen af en sådan (se senere) involverer også delingen af et linjestykke i det gyldne snits forhold - ikke en betegnelse, der blev brugt, men derimod et græsk udtryk, som oversat til dansk er det yderste og mellemste forhold (Engelsk: extreme and mean ratio). Konstruktionen af de fem regulære polyedre er behandlet i Euklids Elementer, bog XIII (se fx. [16], side 463-481).
Pythagoræerne og musikkenAt matematikken så ikke udelukkende forblev en beskæftigelse for de få, skyldes blandt andet, at tallene kom til at spille en rolle indenfor musikken. Pythagoræerne viste dermed, at de ikke blot var i stand til at tænke abstrakt og løsrevet fra virkeligheden, de kunne også inddrage eksperimenter og kombinere det med en abstrakt musikteori. Pythagoræerne anvendte et apparat kaldet en monokord (eller monochord), som består af en enkelt streng, der sidder fastspændt på en resonanskasse (se den næste figur). En skyder kan forkorte strengen og resultere i en anden grundtone, når strengen anslås. Man var interesseret i at studere toneintervaller. Et toneinterval mellem to toner defineres som forholdet mellem tonernes frekvenser. Det viser sig, at frekvensen af den tone, en svingende streng giver anledning til, er omvendt proportional med strengens længde - når den kraft, hvormed strengen er udspændt, er fastholdt. Halveres strengen, vil det altså resultere i en tone med en frekvens, der er dobbelt så stor. Intervallet mellem denne tone og den oprindelige vil derfor være 2 : 1 i frekvens, det vi i dag kalder for en oktav. Pythagoræerne fandt, at hvis man samtidigt anslår to strenge, hvis længder har et forhold som svarer til forholdet mellem to hele tal (fx 2:1, 3:2, etc.), så opnåede man en særlig harmonisk samklang. Særligt kunne de godt lide at anvende tallene 1, 2, 3 og 4, fordi deres sum giver det for grækerne hellige tal 10. Pythagoræernes teorier er afspejlet i det vi i dag kalder en pythagoræisk stemning eller den pythagoræiske skala. Den er karakteriseret ved, at man som udgangspunkt ønsker at alle oktaver og kvinter skal være eksakte, dvs. indeholde de eksakte forhold 2:1 og 3:2. Detaljer kan ses på hjemmesiden Musikipedia.dk om stemningssystemer (se linket [L3] nedenfor) samt i et fint kandidatspeciale af stemningssystemer af Sara Scully (se linket [L4]). Se desuden mine Uddybende kommentarer lidt længere nede på denne side. Den kristne filosof Boëthius (ca. 480-524/25), som var stærkt inspireret af nyplatonismen, søgte at viderebringe arven om Platon og Aristoteles fra det antikke Grækenland til Romerriget. Betegnelsen quadrivium (firevejen) for de fire matematiske kunster aritmetik, geometri, astronomi og harmoni (musik) kan stamme fra ham samt den romerske forfatter Martianus Capellas. Sammen med trivium (trevejen) med de humanistiske kunster gramatik,
logik og retorik, udgjorde quadrivium de syv kunster, som har været et slags dannelsesideal at mestre lige siden den tidlige middelalder. Således har den europæiske musikteori været stærkt inspireret af pythagoræerne, og det har været den eneste matematiske model for de musikalske harmonier helt frem til 1500-tallet.
Fra omkring år 1500 begynder man at eksperimentere med andre stemningssystemer end det pythagoræiske. Det skyldes, at man nu var begyndt at komponere mere avancerede musikstykker, og her opstod problemer med den pythagoræiske stemning. Det førte til opdagelsen af nye brugbare stemninger som blandt andet den rene stemning og senere den ligesvævende stemning. Sidstnævnte er den, der i langtovervejende grad benyttes i den vestlige musik i dag. Jeg skal ikke gå i stor detalje hermed, da det er ret kompliceret. Den interesserede læser kan konsultere linkene [L3] og [L4] eller hæftet [14] nedenfor. Lidt står dog også omtalt under Uddybende kommentarer nedenfor.
Pythagoræerne og astronomienPythagoræeren og filosoffen Philolaus (ca. 470 f.Kr. - ca. 385 f.Kr.) bidrog med et pyrocentrisk verdensbillede, hvori der i centrum af Universet befinder sig en centralild (Central Fire), som vel at mærke ikke er Solen! På koncentriske sfærer (kuglerskaller) og med konstant fart rundt om dette center, bevæger der sig - nævnt i rækkefølge indefra - en antijord eller modjord (Counter Earth), Jorden, Månen, Solen, efterfulgt af de fem planeter Venus, Merkur, Mars, Jupiter og Saturn, som var kendt på den tid. I modellen lyser Solen ikke selv, den reflekterer lys fra centralilden. Yderst sad fiksstjernerne på en himmelkugle. På grund af de sparsomme kilder, hersker der tvivl om detaljerne i modellen. Man mener dog, at han opfattede Jorden og de øvrige himmellegemer som værende runde og kugleformede og ikke flade. Han havde også ret i, at himmellegemer bevægede sig langsommere, jo tættere de er på centralilden. I dag kan det virke mærkeligt og næsten latterligt at indføre en modjord. På den anden side var han på andre områder mere på rette spor: I hans model bevæger Jorden sig, i modsætning til senere verdensbilleder, hvor Jorden er ubevægelig i centrum. Pythagoræerne opfattede planeterne som foretagende periodiske bevægelser, således at alt gentager sig efter en given periode. Det forudsætter at forholdet mellem planeternes omløbstider kan udtrykkes som brøker mellem hele tal. Denne kendsgerning kan være årsagen til, at pythagoræerne fik den set med nutidens øjne mærkværdige tanke, at forsøge at sætte astronomien i forbindelse med musikteorien, hvor forhold mellem hele tal også var grundlaget. Herved opstod læren om sfærernes harmoni. Man gik endda så langt som at postulere, at himmellegemernes regelmæssige bevægelser frembringer regelmæssige uhørbare lyde. Intervallerne mellem disse skulle kunne beskrirves ved hele tal. Ifølge den senere store græske filosof Aristoteles (384 f.Kr.-322 f.Kr.), antog pythagoræerne, at "hastighederne ifølge afstandene svarer til talforholdene i den musikalske harmoni" (se [4]). Vi skal ikke gå nærmere ind på dette her. Den vigtige pointe er her, at pythagoræerne søgte at beskrive planetsystemet ved hjælp af hele tal. Den interesserede læser kan læse mere om musik og astronomi i Hans Buhls lille bog Sfærernes harmoni (se [18]) eller i artiklen Fysik og musik i videnskabshistorien - fra enhed til modsætning (se linket [L5]).
Græsk matematik og filosofi i øvrigtDen store filosof Platon (427 f.Kr.-347 f.Kr.) kom sandsynligvis ikke selv med betydelige bidrag til matematikken. Alligevel kan hans betydning for matematikken ikke overvurderes. Igennem tilskyldelse til at beskæftige sig med matematisk forskning, var han en stor drivkraft, ikke mindst set i lyset af den status Platon havde. Omkring år 385 f.Kr. grundlagde han Akademiet i Athen. Platon opfattede matematikken, med dens fire grene aritmetik, geometri, stereometri og astronomi, som værende den første essentielle ingrediens i træningen af filosoffer. Over døren til hans skole var indskriptionen "ΑΓΕΩΜΕΤΡΗΤΟΣ ΜΗΔΕΙΣ ΕΙΣΙΤΩ", der kan oversættes med noget i retningen af "Lad ingen uegnet til geometri træde ind ad denne dør". Platons akademi tiltrak forskere fra hele den græske verden. Det var opgaver såsom terningens fordobling, cirklens kvadratur og inkommensurable størrelser (irrationale tal), der var i fokus. Platon var blandt andet ven med en af de ledende pythagoræere og matematikere Archytas af Tarentum (428 f.Kr.-ca. 347 f.Kr.). For Platon var praktiske anvendelser at matematik ikke vigtige. Det var derimod de erkendelser, som matematikken afstedkom. Disse kunne rykke sjælen tættere på den absolutte sandhed. Platon skelnede for eksempel mellem en cirkel tegnet af en person i sandet og den ideelle cirkel, som blev håndteret i hovedet. Det var den tænkte og perfekte cirkel, som havde betydning for Platon. I sit akademi havde Platon nogle af tidens bedste matematikere, herunder Theaitetos (ca. 417 f.Kr.-369 f.Kr.) fra Athen og en overgang også Eudoxos fra Knidos (ca. 390 f.Kr.-ca. 337 f.Kr.). Theaitetos skal blandt andet være den første, der angav en konstruktionsmetode for de fem regulære polyedre. Næstefter Archimedes er Eudoxos måske antikkens største matematiske geni. Udover vigtige arbejder i astronomi, er han især kendt for størrelseslæren eller proportionslæren, et genialt greb, hvormed han lykkes med at overkomme den hidtidige barriere med at håndtere forhold mellem inkommensurable størrelser (irrationale tal). Det andet store bidrag er exhaustionsmetoden. Der er tale om en genial metode, hvormed man kan undgå at skulle håndtere uendeligheder eller grænseværdier. Argumenter, som involverede uendeligheder var man ikke glade for dengang: Zenons paradokser er eksempler på de paradokser, som disse kan medføre. Der var ikke blot høje krav til beviser, det var der også til konstruktioner: Platon accepterede for eksempel ikke konstruktioner, som involverede "mekaniske metoder" til tredeling af vinkler, etc. Uden at skulle redegøre for exhaustionsmetoden i detaljer, kan det nævnes, at man med den kan reducere tilsyneladende uendelige processer til endelige. Og det endelige har man styr på. Exhautionsmetoden kan blandt andet bruges til at bestemme arealer og rumfang af komplekse punktmængder. Læseren kan finde mere om størrelseslæren og exhaustionsmetoden i [19]. Desuden havde Platon Aristoteles (384 f.kr-322 f.Kr.) som elev. Denne var dog mere filosof end matematiker, men igen en af historiens betydeligste. Platon og Aristoteles anså det geocentriske verdensbillede som værende det rigtige. I denne model er Jorden i centrum og planeterne bevæger sig med konstant fart i cirkulære baner med Jorden som centrum. Universet blev anset som evig, uforanderlig og i harmoni. Men der er også stor forskel på den måde Platon og Aristoteles betragter verden og naturvidenskaben på, og det vil føre alt for vidt at komme inde på det her. Den interesserede læser henvises til [4].
Platon knyttede desuden (for os i dag underligt) læren om de fire elementer sammen med de regulære polydre (se ovenfor). Jord blev koblet til terningen, vand til ikosaederet, luft til oktaederet og ild til tetraederet. Det femte og sidste regulære polyeder, dodekaederet, koblede han til det himmelske. Alt dette kan læses i Platon's værk Timaios, som er formet som en dialog mellem personerne Sokrates, Timaios,
Hermokrates
og Kritias. Meget tyder på, at tilknytningen af de fire førstnævnte regulære polyedre til de fire elementer allerede var foretaget af pythagoræerne. Vi går nu ind i den hellenistiske periode, hvor centrum for videnskaben flytter fra Athen til Alexandria. I perioden fra 336 f.Kr. til ca. 331 f.Kr. erobrede makedoneren Alexander den store Grækenland, Perserriget, Egypten m. m. Alexander den Store grundlagde byen Alexandria omkring en lille ægyptisk by ved nildeltaet omkring 331 f.Kr. Byen udviklede sig til et betydeligt økonomisk og kulturelt centrum og tiltrak forskere fra hele Middelhavsområdet. Byen havde desuden en slags universitet Museion med oldtidens største bibliotek. Kendskabet til den græske videnskab spredte sig derved vidt omkring og blev ikke standset af romernes ekspansion. Det er nu, at vi kommer til en anden vigtig person fra antikken, nemlig Euklid. Det er stærkt usikkert, hvornår han blev født, men almindeligvis antager man, at han var på sit højdepunkt omkring 300 f.Kr. Han abejdede i Alexandria. Euklids bedrift var at skrive et kæmpe værk, Elementerne, bestående af 13 bøger, hvori han samlede resultater fra en række andre græske matematikere (herunder af pythagræerne, Hippokrates fra Chios, Eudoxos, Theaitetos og mange andre) til et imponerende samlet værk. Han skal have bragt orden i beviser, som kun var løseligt skitseret, rettet fejl med mere. En historie fortæller, at Ptolemaios I Soter - en af Alexander den Stores generaler, som var blevet statholder i Egypten - engang spurgte Euklid, om ikke der fandtes en kortere vej til geometrien end Elementerne, hvorefter Euklid skal have svaret de berømte ord: "Der findes ingen kongevej til geometrien".
Værket blev en sand "bestseller", idet den i mange lande har dannet grundlag for matematik-uddannelsen næsten helt op til i dag. Allerede i oldtiden blev den skrevet af og kom til at findes i flere forskellige versioner, nogle med særlige indledninger eller med kommentarer og tilføjelser (skolier). I middelalderen blev de oversat til arabisk og også til latin. Den første trykte udgave på latin udkom i Venedig i 1482. Det påstås endda, at bogværket kun er overgået af Biblen, hvad angår antallet af forskellige udgaver, den er udgivet i siden trykkekunsten blev indført. Euklids elementer er et fremragende værk til at illustrere betydningen af den axiomatisk deduktive metode. Værket opstiller sætninger og beviser dem på baggrund af aksiomer. Den interesserede kan studere Euklids Elementer nærmere ved at kigge i [16], hvor Elementerne er oversat til engelsk, eller man kan studere den danske oversættelse af Tyra Eibe (se [20]).
Fra den hellenistiske periode skal især nævnes Archimedes (287 f.Kr.-212 f:Kr.). Han betragtes normalt som oldtidens største matematiker og videnskabsmand. Som ung studerede han i Alexandria, men tilbragte ellers det meste af sit liv i byen Syracus på Sicilien. Ikke blot skrev han bøger om et væld af matematiske emner, han grundlagde også det, man kan kalde den matematiske fysik. Hvad angår sidstnævnte, skrev han om statik (Om plane figurers ligevægt) samt hydrostatik (Om legemer der flyder på vand). Teorien blev endda søgt aksiomatiseret. Udover det er Archimedes kendt for at have gjort en række ingeniøragtige opfindelser (han skrev dog aldrig om dem), herunder talrige maskiner til forsvar af Syracus, samt skruen til at løfte vand op med (Archimedes' snegl). Han er også kendt for sætningen "Giv mig et fast punkt, så vil jeg bevæge Jorden" (vægtstangsprincippet). Archimedes kom også med flere bidrag i astronomi. Det vil føre for vidt at komme ind på det væld af matematiske resultater, som kom fra hans hånd. Archimedes udviste igennem sine matematiske idéer og beviser stor originalitet, og med sin ekstreme stringens lever han op til de højeste standarder på den tid. I 1906 gjorde den danske filolog J. L. Heiberg (1854-1928) og professor ved Københavns Universitet, en bemærkelsesværdig opdagelse i Konstantinobel (nu Istanbul): Et værk på pergament var blevet overskrevet med en kristen religiøs tekst. Det underliggende, som kunne ses igennem, viste sig at indeholde et værk af blandt andet Archimedes (Archimedes' Palimpsest). Skriftet indeholdt sensationelt et på det tidspunkt ukendt værk af Archimedes, nemlig Metoden, hvori han beskriver en genial metode til at bestemme arealer og rumfang af ukendte områder/legemer ved et slags vægtstangsargument. Siden kunne han bevise opdagelserne stringent ved exhaustionsmetoden, stammende fra Eudoxos. Archimedes var så glad for sin opdagelse af at rumfanget af en kugle indskrevet i en cylinder med samme højde som diameter er 2/3 af rumfanget af cylinderen, at han bad om at få en kugle indskreven i en sådan cylinder anbragt på sit senere gravmæle. På trods af at romerne blev forsinket som følge af de smarte maskiner, Archimedes havde opfundet, så blev Syracus indtaget ved en storm på byen i året 212 f.Kr., ledet af Marcellus. Archimedes blev dræbt af en romersk soldat. En myte fortæller, at han skal have sagt til en romerske soldat: "Forstyr ikke mine cirkler", mens han tegnede i sandet. Herefter skal soldaten have dræbt ham. Romeren Marcus Tullius Cicero (106 f.Kr.-43 f.Kr.) fandt graven overgroet med vegetation
halvandet hundrede år senere. Mens den hellenistiske periode betragtes som en nedgangstid for kunst- og filosofihistorien, så er den et højdepunkt for matematikken og astronomien. Udover Euklid og Archimedes, var der også Apollonius af Perga (ca. 262 f.Kr.-190 f.Kr.), som skrev en stor betydende bog om keglesnit, samt Eratosthenes fra Kyrene (274 f.Kr.-194 f.Kr.), der var astronom og matematiker og blandt andet bestemte Jordens omkreds med en fejl på kun omkring 10%. I året 30 f.Kr. erobrede Oktavian - den senere romerske kejser Augustus - byen Alexandria. Det gjorde arbejdsforholdene dårligere for de græske videnskabsmænd. Romerne var ikke praktiske folk. De havde ingen interesse i at støtte den græske videnskab, hverken i Alexandria, i Grækenland eller i andre dele af deres imperium. Alligevel lykkedes det den græske matematiker og især astronom Klaudios Ptolemaios (eller Claudius Ptolemæus) (ca. 100-ca. 170) over 100 år efter romernes magtovertagelse at skrive og udgive sit imponerende værk Almagest, som blev den vigtigste kilde til astronomien i de næste mange århundreder. I Almagest arbejder Ptolemaios dog stadig med det gamle (forkerte) geocentriske verdensbillede, nu blot med de cirkulære planetbaner udskiftet korrigeret med epicykler. Ptolemaios' værk var det man støttede sig til helt indtil renæssancen, hvor Nicolaus Kopernikus (1473-1543) opstillede det heliocentriske verdensbillede med Solen i centrum. Også Tycho Brahes observationer fra slutningen af 1500-tallet, der forbedrede de gamle observationer af himmellegemerne med en faktor 10, bidrog til at man ændrede det hidtidige gamle verdensbillede.
SammenfatningPythagoræerne søgte med deres specielle naturfilosofi at forbinde alt i naturen og musikken med hele tal. De søgte harmonien og regelmæssigheden. Platon førte denne tradition videre. Det himmelske, det guddommelige blev studeret. Ifølge Platon er de materielle foranderlige ting i verden kun ufuldkomne kopier af de rene uforanderlige idéer. Det er filosoffens opgave at studere disse idéer, og her er matematikken til stor hjælp. Først handlede alt om forholdet mellem hele tal. Da pythagoræerne opdagede de irrationale tal (inkommensurable størrelser) bragte det umiddelbart kaos i deres forestillingsverden, men den store græske matematiker Eudoxos fik sat skik på det gennem sin størrelses- eller proportionslære. Man kan så sige, at det er paradoksalt, at det tal, som er temaet på denne side, og som nogle har forbundet med det himmelske og det guddommelige, netop er et irrationalt tal! Men netop denne kendsgerning er vel også medvirkende til at gøre emnet ekstra interessant.
Uddybende kommentarerJeg vil slutte afsnittet med oldtiden af med nogle kommentarer, særligt til den del, som handler om musikken. Lad os lige repetere pointen med monochorden (egentlig dichorden), hvor pythagoræerne oplevede harmoni, når de anslog to strenge, hvis længdeforhold svarer til forholdet mellem to hele tal - helst små tal. Her er det vel at mærke antaget, at de to strenge er spændt lige hårdt ud! Længdeforholdene kunne for eksempel være 1:2, 2:3, 3:4, etc. I dag ved vi, at frekvensen af den lyd, som
frembringes ved at anslå de to strenge, er omvendt proportional med strengenes længder, dvs. frekvensforholdene mellem de tre ovenfornævnte par af strenge vil være henholdsvis 2:1, 3:2 og 4:3 - de forhold, som i dag betegnes en oktav, en kvint og en kvart. De harmoniske forhold med navne er vist på figuren herunder. Til højre på figuren har jeg af pædagogiske grunde afbildet en del af et klaver, så man kan se, hvorledes man på et nutidigt klaver kan frembringe (næsten) det
samme frekvensforhold mellem de to toner. Når jeg siger "næsten" skyldes det, at det afhænger lidt af, hvordan klaveret er stemt. Normalt vil oktaven, som fås ved at gå 12 tangenter mod højre (de sorte tangenter medregnet), være eksakt. Kvinten fås ved at gå 7 tangenter mod højre, etc.
Hos pythagoræerne fandt man altså harmonien i forholdene mellem to hele tal. Det blev dengang ved "talmagi". Det er ikke underligt, at man senere begyndte at fundere over, hvorfor tonerne lyder harmonisk sammen ved disse forhold. Man kan blive meget klogere på det ved at studere den udmærkede lille bog [18]. I den lange fortælling stiller man sig ikke overraskende det spørgsmål, hvad lyd egentligt er, og hvordan lyd frembringes. Det skal lige nævnes, at man snakker om konsonans, når de to toner lyder harmoniske sammen, mens man kalder det dissonans, når de lyder uharmoniske sammen. Den franske fysiker Joseph Sauveau (1653-1716) fandt for eksempel, at en streng udover sin grundfrekvens også kan have andre frekvenser for oversvingningerne. Det kan illustreres som på figuren herunder, hvor grundsvingningen er afbildet sammen med en række oversvingninger.
Det skal i den forbindelse præciseres, at grundsvingningen og oversvingningerne eksisterer på samme streng og samtidigt! I moderne matematisk/fysisk terminologi vil man sige, at man opnår den totale bølgefunktion ved at lægge bølgefunktionerne for de enkelte oversvingninger sammen (Superpositionsprincippet). I dag kan man faktisk også "gå den modsatte vej" ved at rekonstruere grundsvingningen og oversvingningerne, hvis man har bølgefunktionen for det samlede lydbillede. Det gøres
ved den såkaldte Fourieranalyse, opkaldt efter den franske matematiker og fysiker Jean Baptiste Joseph Fourier (1768-1830). Det er dog alt for kompliceret til at blive omtalt nærmere her. Med denne fysiske indsigt bliver det mere forståeligt, hvorfor man opfatter to toner, som værende i større indbyrdes harmoni, når forholdet mellem deres frekvenser er som forholdet mellem to hele tal. Disse heltallige frekvensforhold findes nemlig allerede fysisk set: Frekvensforholdet mellem grundtonen og 1. overtone er som 2:1 ligesom frekvensforholdet mellem 1. overtone og 2. overtone er som 3:2, etc. Men opfattelsen af harmoni handler også om menneskets perception og er kompliceret.
Fysikeren og fysiologen Hermann von Helmholtz (1821-1894) udgav i 1863 et monumentalt værk Die Lehre von der den Tonempfindungen als physiologische Grundlage für die Theorie der Musik. Han var interesseret i at forstå, hvordan øret og hjernen opfatter lyd og især musik. Den lidt yngre fysiker Lord Rayleigh (1842-1919) udførte ligeledes en række eksperimenter. I hans store reviderede værk The Theory of Sound fra 1894 gav han en matematisk teori for for akustikken. Disse to forskere
lagde i høj grad grunden til den moderne teori for akustik (se evt. [18]). At konstruere en toneskala består overordnet i at finde en række toner, hvis frekvensforhold giver en høj grad af indbyrdes konsonans, dvs. skalaen skal indeholde mange toner, som lyder harmoniske sammen. Oversat til frekvens, gav pythagoræerne os, at det gælder om at have toner, hvis frekvensforhold er som forholdet mellem (helst små) hele tal. Her er frekvensforholdene 2:1 (oktav) og 3:2 (kvint) højt ønskede. Som regel er oktaven basis for enhver musikskala. Man ønsker derefter at opdele en oktav i en række mellemliggende toner. Spørgsmålet er, hvor mange toner, den skal inddeles i, og hvilken frekvens hver node skal have? Det viser sig desværre ikke at være simpelt. Faktisk findes der ikke nogen ultimativ bedste løsning på den opgave. Basis for den pythagoræiske skala, som blev anvendt helt op til renæssancen, er at oktaverne og kvinterne skal være eksakte. I Vesten bruger vi 12 (halv)-toner i hver oktav. De nævnte krav kan for eksempel føre til følgende mulige Pythagoræiske stemning for et klaver:
Som nævnt anvendte man den pythagoræiske stemning helt op til renæssancen, hvor musikken efterhånden blev så kompliceret, at man ikke længere kunne leve med fx ulvekvinten i den pythagoræiske stemning. Det førte til konstruktionen af den rene stemning, og senere kom endda middeltone-stemningen til. Disse to stemninger skal jeg dog ikke komme nærmere ind på her, blot henvise den interesserede læser til den fine hjemmeside musikipedia.dk ([L3]. Men også disse to stemninger har ulemper. Det har bevirket, at man i dag benytter den ligesvævende stemning. Den er matematisk simpel, idet man deler oktaven i 12 lige store intervaller, forstået på den måde at to efterfølgende noder altid får samme indbyrdes frekvensforhold. Det må nødvendigvis blive den tolvte rod af 2, som i decimaler er 1,0594663094. Så man har forladt idéen om at frekvensforholdene skal være brøker mellem hele tal - nu er det irrationale tal! Ulempen er, at man har måttet opgive kravet om fx en eksakt kvint. Heldigvis udmærker antallet 12 halvtoner sig ved at give kvinter, kvarter og tertser, som ligger tæt på de eksakte brøker, som nedenstående figur viser. Den store fordel ved den ligesvævende stemning er, at der nu ikke er nogle frekvensforhold, som er helt uharmoniske. Det er desuden blevet betydeligt nemmere at transponere et musikstykke til en anden toneart.
Det er et nærliggende spørgsmål at stille sig, hvad der gør valget af 12 halvtoner i en oktav specielt. Kunne man tænke sig et andet antal, som er lige så godt eller bedre? Ja så skal man helst have et helt antal kvinter til at være lig med et helt antal oktaver. Vi ved det er umuligt på grund af entydig primfaktoropløsning, men vi kan komme med en approksimation. Man kan argumentere som på figuren nedenfor: Vi tager totalslogaritmen på begge sider af ligningen til venstre. Det giver betingelsen,
at totalslogaritmen til 3/2 skal være et rationalt tal n/m. De bedste rationale approksimationer til et reelt tal (underforstået med mindst mulig nævner), er dem, som man får ved at udvikle det reelle tal i en kædebrøk. Den vil naturligvis være uendelig, da tallet er irrationalt, men hvis vi skærer kædebrøken af forskellige steder, får vi følgende stadig mere præcise approksimationer: 1, 1/2, 3/5, 7/12, 24/41, 31/53, 179/306, ...
Vi genfinder her 7/12, som vi allerede kender. Men vi ser, at man også kunne lade der være 41 tangenter eller 53 tangenter i hver oktav! Det giver selvfølgelig noget at holde styr på rent praktisk, men ifølge [L7], udførte den engelske musikteoretiker Robert Bosanquet i 1876 et generalized keyboard med 53 tangenter i en oktav.
3. Leonardo af Pisa og Fibonacci-talleneVi bevæger os til Norditalien i begyndelsen af 1200-tallet. Leonardo af Pisa (ca. 1170-ca. 1250), eller som han også blev kaldt, Fibonacci, var søn af en forretningsmand og embedsmand. Pisa var dengang en livlig handelsby, hvor man blandt andet handlede med krydderier fra Fjernøsten. Den megen handel krævede bogføring af lagre og priser. At regne med romertal er langt fra effektivt. At lægge sammen og trække fra går lige an. At gange tal sammen er håbløst. Det hjalp dog lidt, at man kunne regne på kuglerammer, men det uhensigtsmæssige talsystem var en stor hæmsko. Leonardo hjalp i en periode sin far som handelsmand og toldfunktionær i Bugia i det nuværende Algeriet, og rejste senere til flere andre Middelhavslande. Her stiftede han bekendtskab med det hindu-arabiske talsystem, som han erfarede var alle andre talsystemer overlegent. Efter at have fået udvidet sin matematiske horisont, gik han i gang med at skrive en bog, hvori han beskrev, hvordan man kan anvende det hindu-arabiske talsystem i praksis. Bogen indeholder et væld af eksempler, som spænder lige fra hestekøbsopgaver til tømning og fyldning af cisterner. Leonardos bog med navnet Liber Abaci udkom i år 1202. Han høstede stor anerkendelse for værket. Den var et kærkomment bidrag til matematikken i Vesteuropa, som på den tid var meget tilbagestående, ikke mindst som en følge af kirkens store dominans. Men tilbage til Liber Abaci. Grunden til, at bogen omtales her er, at der er en helt særlig opgave fra kapitel XII: udviklingen af antal kaniner i en kanin-population. Som man måske kan gætte, har den forbindelse til det gyldne snit!
Et par kaniner (en han og en hun) føder et nyt par kaniner hver måned. Nyfødte kaniner bliver dog først kønsmodne efter 2 måneder. Vi starter med ét par nyfødte kaniner. Efter 1 måned er de blevet større, men stadig ikke kønsmodne. Derfor er der stadig kun ét par. Efter 2 måneder er parret kønsmodent og får et nyt par som afkom. Sammen med det oprindelige par er der dermed to par. Efter 3 måneder føder det oprindelige par igen et nyt par, mens det andet par ikke er fødedygtigt endnu. Sådan fortsættes måned efter måned. Skematisk kan det stilles således op:
Selv om opgaven er meget urealistisk, fik den alligevel stor opmærksomhed, eftersom den har teoretisk interesse. Udviklingen måned efter måned i kaninbestanden kan nemlig beskrives ved en rekursiv talfølge. Hermed menes en talfølge, hvor man kan bestemme det nye tal i talfølgen ud fra kendskab til de forrige. Vi skal ikke gå nøje ind i de matematiske argumenter her. Den interesserede læser henvises til noten med arbejdsopgaver i næste afsnit. Det viser, at hvis vi lader Fn betegne det samlede antal kaninpar efter n-1 måneder, så følgende rekursive formel, hvoraf man kan udregne antallet af kaninpar i en given måned ud fra viden om antallet af kaninpar i de forrige to måneder:
Givet antallet af kaninpar fra start og efter 1. måned, kan vi altså regne alle de efterfølgende antal kaninpar ud skridt for skridt:
Vi får altså følgende følge af tal måned for måned, som udgør den såkaldte Fibonacci-følge: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, ... Hvert nyt tal fås ved at addere de to forrige tal i rækken. Et nærliggende spørgsmål er, om man er nødt til først at udregne fx de 999 første Fibonacci-tal før man kan udregne Fibonacci-tal nummer 1000? Svaret er nej. Der eksisterer faktisk en lukket formel for det n'te Fibonacci-tal, nemlig følgende:
Det viser sig, at forholdet mellem to på hinanden følgende Fibonacci-tal nærmer sig til det gyldne snit, når n går mod uendelig. Egenskaben blev i 1611 opdaget af den berømte tyske astronom Johannes Kepler (1571-1630), som vi skal kigge nærmere på i et senere afsnit. Konvergensen mod det gyldne snit blev dog først bevist langt senere.
Så hvad der fra start var en urealistisk model for udviklingen af en kaninbestand, skulle vise sig at have stor betydning. det viser sig, at der gælder en sand sværm af smukke relationer involverende Fibonacci-tallene. Faktisk så mange, at der findes et tidsskrift Fibonacci Quarterly, hvori man studerer disse smukke egenskaber. Vi skal ikke komme nærmere ind på dem her. Du kan se lidt nærmere på nogle få af dem i noten i næste afsnit. Her er også et stringent bevis for, at tallene i Fibonacci-følgen konvergerer mod det gyldne snit. Ikke nok med, at talfølgen har en vigtig plads i matematikken. Det viser på forbløffende vis, at de forekommer i naturen, fx i solsikker (se senere afsnit), ananas og meget andet.
4. En note med arbejdsopgaverJeg har udarbejdet en lille note om det gyldne snit, både med information om, hvad det handler om, men også med opgaver, hvor læseren skal løse nogle opgaver eller konstruere nogle figurer for bedre at kunne forstå stoffet. Måske det kan bruges i et forløb eller projekt i gymnasiet?
5. Pentagonen og andre gyldne figurerSom sædvanlig interesserer vi os for at konstruere med passer og lineal, ligesom de gamle grækere. At dele linjestykket AB nedenfor i det gyldne snits forhold kan gøres på følgende måde: Man oprejser den vinkelrette linje m i punktet B (detaljer om denne standardkonstruktion kan ses i noten i afsnit 4). Man konstruerer midtpunktet M på linjestykket AB (igen standardkonstruktion). Afstanden BM tages i passeren, og der tegnes en cirkelbue til skæring med den vinkelrette linje m i et punkt, vi vil kalde C. Punkterne Aog C forbindes med en linje. Med centrum i C og afstanden CB i passeren tegnes som vist en cirkelbue, der skærer linjestykket AC i et punkt, vi kalder D. Endelig tager man afstanden AD i passeren og tegner en cirkelbue med centrum i A. Cirkelbuens skæringspunkt S med AB er det søgte punkt. I noten i afsnit 4 er det en opgave for læseren at vise - blandt andet ved brug af Pythagoras' sætning - at vise, at punktet S virkelig deler linjestykket AB i det gyldne snits forhold, eller bare det gyldne forhold.
Den gyldne femkant (pentagon)En af de mest kendte figurer, hvori det gyldne snit indgår, er den regulære pentagon, dvs. en femkant, hvor alle siderne er lige store og hvor de fem hjørner alle ligger på en omskreven cirkel. Man kan vise, at to diagonaler skærer hinanden i det gyldne forhold. Tegner man kun diagonalerne, får man det såkaldte pentagram. Pythagoræerne brugte pentagrammet som deres hemmelige logo for at ønske hinanden sundhed og lykke.
Pentagrammet er igennem tiderne benyttet i forskellige former for magi. I så henseende skulle pentagrammet som vist ovenfor "stående" på de to spidser påkalde oververdenens ånder, mens pentagrammet spejlet i en vandret linje (med spidsen nedad) påkalder sig ånder fra underverdenen. Vi er altså i det okkulte! De femtakkede stjerner indgår ellers både i USA's flag Stars and Stripes og i EU's flag. Hvad angår pentagonen til venstre, så er det netop geometrien i USA's
forsvarsministerium Pentagon, beliggende i Arlington i staten Virginia. Hvordan man helt konkret kan konstruere en pentagon er antydet på figuren nedenfor. Konstruktionen er nærmere forklaret i noten i afsnit 4. Spørgsmålet er, hvilke regulære polygoner, som kan konstrueres med passer og lineal? Grækerne kendte til konstruktion af en regulær n-kant for tilfældene n = 3 og n = 5, men ikke for andre primtalsværdier af n. Det var en stor overraskelse, da det lykkedes for en af de største matematikere gennem tiderne, tyskeren Carl Friedrich Gauss (1777-1855) at konstruere den regulære 17-kant med passer og lineal. Det skete i 1796, da han kun var 18 år gammel!
I 1801 udgav Gauss sit berømte værk Disquisitiones Arithmeticae, hvori han blandt andet gav en fuldstændig klassifikation af hvilke regulære polygoner, det er muligt at konstruere med passer og lineal:
Gauss beviste dog ikke nødvendigheden i sætningen, kun tilstrækkeligheden. Pierre Wantzel gjorde beviset færdigt i 1837. Derfor går sætningen under navnet Gauss-Wantzels Theorem. Fermat primtallene er i øvrigt: 3, 5, 17, 257, 65537, 4294967297, 18446744073709551617, ... Så der er langt imellem disse primtal. En metode at konstruere en regulær 17-kant på kan i øvrigt findes i [23] og [24].
|
|
Ligesom Gud er kvintessensen i relation til jord, vand, luft og ild ..., giver vores forhold ... formel eksistens til selve himlen ifølge Platon, som i Timaios tilegner dodekaederet til den. |
Timaios er en af Platons berømte dialoger. Som nævnt illustrerede Leonardo da Vinci Pacolis bog. I blandt tegningerne var en illustration af et dodekaeder. Det forekommer, at Leonardo faldt for udtrykket det himmelske forhold, og han benyttede det senere i en af sine egne bøger, dog uden dermed specifikt at hentyde til det gyldne snit. Det var snarere en betegnelse for smukke forhold i al almindelighed. Det er her, at forskellige misforståelser muligvis kan være opstået
om, at der blev opfordret til at bruge det gyldne snit i kunsten. Man ved det ikke. Artiklen [3] kommer med forskellige spekulationer om, hvordan det kan være, at myterne om det gyldne snit er dukket op i kunsten.
Eftersom der ikke er fundet skriftlige kilder fra før midten af 1800-tallet, som omtaler brugen af det gyldne snit i forbindelse med arkitektur, skulturer og malerier, tvivler en del historikere på, at det gyldne snit har været anvendt bevidst i kunsten før midten af 1800-tallet. Efter dette tidspunkt dukkede myten om den tidlige brug af det gyldne snit i kunsten op oftere og oftere. Det blev især båret frem af den tyske filosof Adolf Zeising, samt to tyske matematikere Hermann Hankel og Moritz Cantor, som var interesserede i deres fags historie. Især de to sidstnævnte kom med udokumenterede påstande om, at det gyldne snit var blevet anvendt bevidst i kunsten i antikken og middelalderen. Mere herom kan læses i artiklen [3]. Vi vælger hermed at konkludere, at der ikke synes at være nogen dokumentation for bevidst brug af det gyldne snit i kunsten før midten af 1800-tallet! Måske en skuffelse for nogen. Det behøver det nu ikke være, for det gyldne snit leverer ved det simple princip, hvorved det er defineret (det lange stykke (summen) forholder sig til det lange stykke, som det lange til det korte), et væld af interessant matematik. Ligesom historien om det gyldne snit også er fascinerende. Historien behøver ikke udokumenterede påstande om dets brug.
En af grundlæggerne af den moderne psykologi, Gustav Theodor Fechner (1801-1887), foretog en undersøgelse med henblik på at verificere eller afkræfte Zeisings påstande om, at det gyldne snit er særligt behageligt at kigge på. Undersøgelserne inkluderede spørgeundersøgelser, statistik og eksperimenter. Nogle gange faldt resultatet ud til fordel for teorien om, at det gyldne snit er det mest æstetiske, andre gange var resultaterne tågede. Utallige forsøg har siden været udført af diverse personer, og der er ingen konklusion. Ofte bliver undersøgelserne kritiseret for ikke at ligestille alle udfald.
Nedenfor har jeg lavet min egen lille test: Læseren opfordres til at vælge det rektangel, som forekommer at have de mest æstetiske proportioner. Netop et af rektanglerne har det gyldne snits forhold. Nogle af de andre har også interessante forhold.
Hvilket forhold er gyldent?
Det skal tilføjes, at litteraturen indeholder mange eksempler på påståede brug af det gyldne snit i diverse kunstværker, herunder i malerier, arkitektur såsom Parthenon i Athen og i fx pyramider i Egypten. Da der imidlertid ikke er nogen evidens for, at skaberne skal have tænkt på det gyldne forhold (jf. artiklen [3]), så undlader vi at give eksempler herpå. I praksis kan man nemlig ofte få gyldne rektangler til at passe sådan nogenlunde i dele af malerier og i arkitektur ved rene tilfælde - endda med ret stor sandsynlighed, fordi der er så mange måder at anbringe rektanglet på!
Lad os for en fuldstændigheds skyld også nævne brugen af harmoniske forhold i kunsten, også selv om det ikke direkte har noget med det gyldne snit at gøre. Faktisk betød harmoniske forhold i antikkens musikteori, som vi allerede har set i afsnit 2, forhold mellem hele tal, for eksempel 2:1, 3:2, 4:3, etc. Det er værd at bemærke, at det ikke inkluderer det gyldne snits forhold, eftersom sidstenævnte er et irrationalt tal, ikke et rationalt tal, som de øvrige. Den store italienske arkitekt, forfatter, renæssance-humanist poet, præst, filosof m.m. Leon Battista Alberti (1404-1472) opbyggede i sin afhandling om arkitektur De re aedificatoria en teori om proportioner (se evt. [21]). Som grundlag havde den Vitrivius teorier (se nedenfor). Alberti agiterede i bogen for idéen om, at en bygning skal udgøre et harmonisk hele, og at enhver del af bygningen skal være integreret i hele dets design. For at nå dette mål, måtte arkitekterne lade sig lede af et system af proportioner med høj æstetisk tiltrækningskraft. Proportioner, som har rod i Guds harmoniske Univers. Her kom matematiske principper i spil. Han tænkte specielt på pythagoræernes musikteori, og som han anførte: "Talforhold, som påvirker vores ører med glæde, er de samme som glæder vores øje og sind". Alberti overtog således teorien for musikkens konsonanser i sin arkitektur. Hans syn på arkitekturen blev retningsgivende for renæssancens arkitekter. Fra at være et lavere værdsat erhverv at være arkitekt, blev det højnet fra en manuel til en intellektuel disciplin. Musik blev betragtet som en matematisk videnskab, og den var en del af firvejen (quadrivium), som repræsenterede færdighederne aritmetik, geometri, astronomi og musik. Vi skal ikke gå nærmere ind i, hvordan der blev argumenteret i musikteorien, blot at det førte Alberti til følgende liste af heltal (se [21]):
1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 27, 32, 36, 48 og 54
Brugte en arkitekt tal fra denne liste i det rumlige design af sin bygning, så vidste han, at han videregav den samme harmoniske orden til sit design, med hvilket Gud skabte Universet. Den senere mesterarkitekt i renæssancen, Andrea Palladio, udnyttede de grundlæggende geometriske idéer fra Vitrivius samt tallene fra Albertis teori, i sit design af Basilica Palladiana i byen Vicenza.
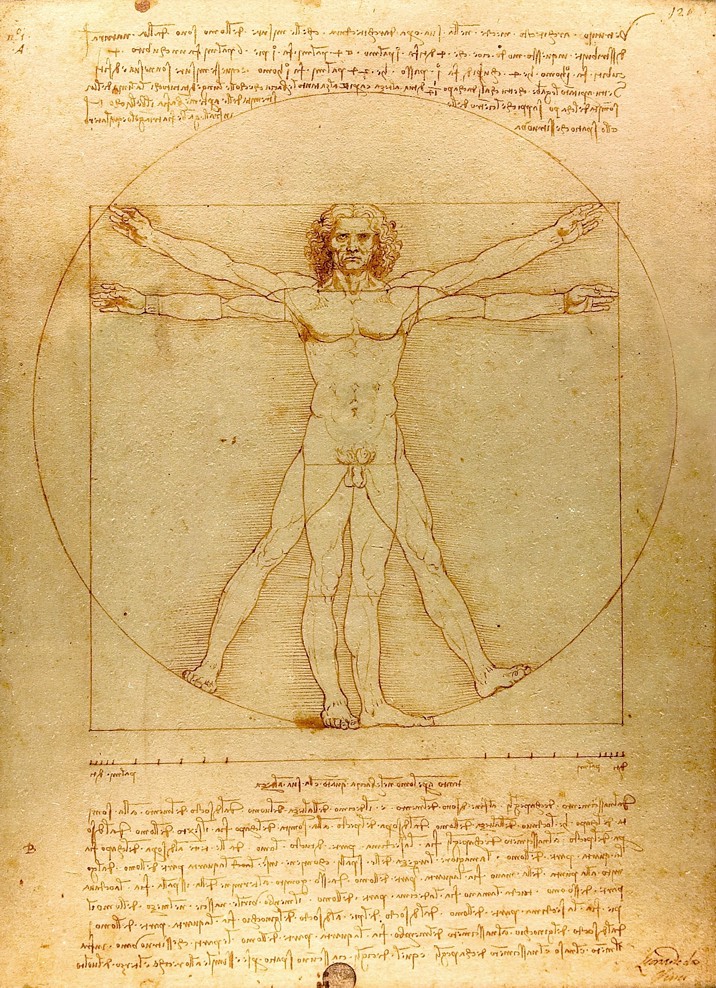
Marcus Vitruvius Pollio (Ca. 75 f.Kr.-ca. 15 f:Kr.) - ofte bare kaldet Vitrivius eller Vitruv på dansk - var en romersk arkitekt og ingeniør. I hans store væk De architectura, som er skrevet ca. 35 f.Kr. og genfundet i 1414, behandler Vitruv arkitektur som en imitation af naturen. Det fik ham til at studere menneskekroppen som et slags ideal. Det førte i renæssancen til, at Leonardo da Vinci udførte den berømte tegning, forstillende Vitrivius-manden. Som figuren af omtalte tegning nedenfor viser, så indskrev Leonardo en mand i både et kvadrat og en cirkel. Førstnævnte demonstrerer, at mandens højde og hans armes længde fra fingerspids til fingerspids forholder sig som 1:1. Altså ikke noget med det gyldne snit her.
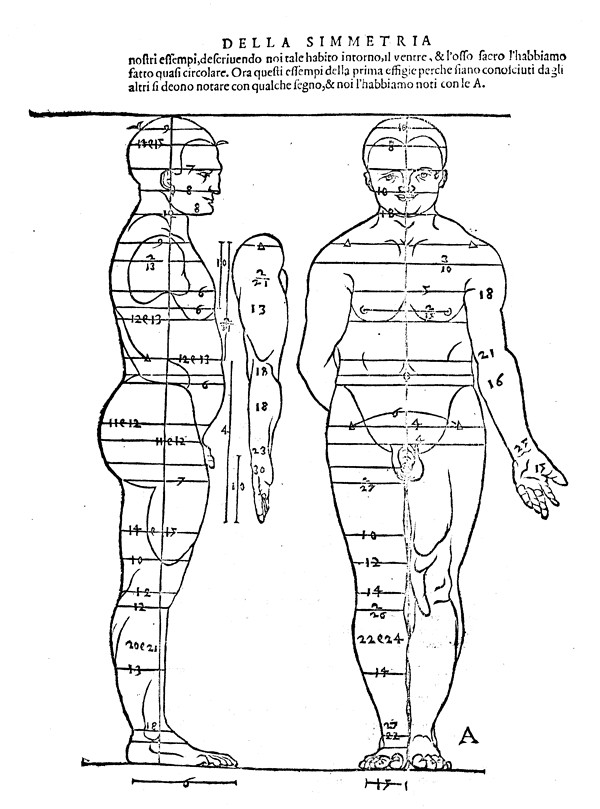
Den største tyske kunstner fra renæssancen, Albrect Dürer (1471-1528), studerede ligeledes menneskets proportioner. Efter flere rejser til Italien og møder med kunstnere der, blev han stærk inspireret. Han blev bekendt med Paciolis illustrationer af en maskulin og en feminin figur konstrueret ud fra geometriske principper. Dürer udgav blandt andet fire bøger om proportioner, hvoraf nogle byggede på Vitruvius teorier, andre på egne empiriske undersøgelser. Han skrev også om skønhedsidealer. Skønt han ikke kunne godtage Albertis begreb om "objektiv skønhed" og i stedet foreslog et relativt begreb baseret på variation, så mente han, at sandheden var skjult i naturen. Under sine rejser til blandt andet Italien blev han overbevist om matematik som værende "den mest præcise, logiske og grafisk konstruktive af alle videnskaber", og derfor en vigtig del af kunsten (se [22]). Hvad angår det gyldne snit, så blev det kun indirekte bragt på banen i en af hans bøger via hans beskrivelser af konsultationer af pentagonen og de platoniske legemer.
Efter midten af 1800-tallet er der - takket være den store røre, der blev skabt om emnet - kunstnere, som bevidst anvendte det gyldne snit i deres kunst. En af dem er Le Corbusier, som er kunstnernavnet på den schweiziskfødte arkitekt, møbeldesigner, byplanlægger, forfatter, skulptør og kunstmaler Charles-Édouard Jeanneret-Gris (1887-1965). Han studerede det gyldne snit og brugte det i sine produktioner. Blandt andet har han skabt proportionssystemet Modulor, som han brugte som skala i mange af sine bygninger. The Modulor er et forsøg på at opdage størrelsesforhold i den menneskelige krop, inspireret af Leonardo da Vincis Vitruvius mand samt andre italienske renæssance kunstnere, herunder Leon Battista Alberti. Og som sagt desuden inkluderende det gyldne snit.
Den spanske kunstner, Salvador Dalí (1904-1989), skal desuden bevidst have anvendt det gyldne snit i hans berømte maleri Sacrement of the Last Supper. Maleriets dimensioner er som det gyldne snit, og som et centralt element er der i maleriet desuden afbildet et dodekaeder, der ifølge Platon repræsenterede det guddommelige/himmelske (se afsnit 2). Dodekaederet indeholder regulære femkanter (pentagoner) som sideflader, og det gyldne snit er tæt forbundet til pentagonen (se afsnit 5).
Der er folk i dag, som ved beskæringer eller i kompositioner tænker nøje over placeringerne af vigtige genstande i et billede. Værktøjer hertil er endda lagt ind som standard i Adobe Photoshop. Vælges beskæringsværktøjet (Engelsk: Crop), får man i værktøjslinjen adgang til Maskeindstillinger.
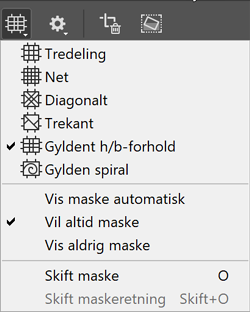
Der er blandt andet Gyldent h/b-forhold, Tredeling samt Gylden spiral. De øvrige, herunder værktøjer til at styre skrålinjer, ser vi bort fra i denne omgang. Lad os se på, hvordan de tre nævnte redskaber hver især er definerede matematisk set. I alle tilfælde benytter man som grundflade et rektangel med længde L og højde H.
Hvad angår det Gyldne forhold, så anbringes her to vandrette og to lodrette linjer midt i billedet. Hvis vi ser på de lodrette linjer, så er forholdet mellem længden L og hver af de de to lodrette linjers afstand til den fjerneste lodrette kant lig med det gyldne snits forhold. Afstanden fra de lodrette linjer til den fjerneste lodrette kant er dermed ca. 0,6180 ganget med længden L. Noget tilsvarende kan siges om de vandrette linjer.
Tredelingsreglen (Engelsk: Rule of Thirds) med at inddele rektanglet i tre lige store dele i både længden og højden er især indført, fordi det er nemmere at håndtere end de vandskelige tal i det gyldne snit.
Matematikken i den gyldne spiral er gennemgået i afsnit 5. Det skal dog nævnes, at vi her tillader skalering i længde og højderetning - ellers skulle man have benyttet et gyldent rektangel, med dets helt specielle forhold mellem siderne.
I det følgende demonstres brugen af de tre standard-værktøjer i Adobe Photoshop: Gyldent h/b-forhold, Tredeling samt Gylden spiral.
Bemærk, at man ved at klikke på billederne nedenfor får et fuldt skærmbillede!
Interfacet i Photoshop til beskæring:
Linjerne er tynde, så det kan være nødvendigt at klikke på billedet for en forstørrelse, for ordentligt at kunne se inddelingerne. Idéen er så, at vigtige elementer i billedet skal "fungere" indenfor de ni felter eller i de fire skæringspunkter. Bemærk, at man ved brug af værktøjet kan flytte rundt på rammen og/eller trække i håndtagene, så man får en beskæring, som får indholdet i de ni felter til at være fornuftig. De gule pile peger på de linjer, som er meget tynde ...
Anvendelse af tredelingsreglen - på engelsk kaldet Rule of Thirds - ser således ud:
Endelig er der værktøjet Gylden spiral, som giver nedenstående resultat: Man ser, at spiralen, som konvergerende snor sig ind mod et fokuspunkt, her et sted i lærredet nederst til venstre, udpeget af den gule pil.
Billedet af nogle tegnere og kunstnere taget på Piazza Navona i Rom ender med efter ovenstående beskæring at se således ud:
Til sidst skal det demonstreres, at man også kan bruge værktøjet brugerdefineret form (Engelsk: Custom Shape) til at beskære billeder i Adobe Photoshop ved hjælp af for eksempel en gylden spiral. Derved kan man få tegnet en maske af en gylden spiral, som kan hjælpe én til en fornuftig beskæring:
Efter indsættelse af den brugerdefinerede form, ses følgende resultat:
Vi ser, at der er mange muligheder for at beskære et billede, så vigtige dele af billedet fremhæves. Hvilke redskaber, der helt præcist skal bruges, er åbent. Man skal desuden være klar til at bryde reglerne, hvis det taler for det konkrete billede.
Vi så på Fibonacci-tallene i afsnit 3. Udover at disse tal blev til i et urealistisk eksempel om kaniners formering i Fibonacci's berømte bog Liber Abaci, så er tallene også berømte på grund af, de dukker op i så mange uvante situationer. Stamtræet fra en drone (hanbi) udvikler sig således efter en Fibonacci talfølge. Et andet eksempel er energitilstandene i en elektron (se [22]). Ikke nok med det: Fibonacci-tal genfindes i planter! Når blade gror på en kvist, eller grene gror på
en stamme, så gør de det på en måde, så der opnås optimal adgang til lys, regn og luft. Det ville for eksempel være uhensigtsmæssigt for grene at placere sig over hinanden. Typisk spiralerer de op langs stammen. At naturen således automatisk optimerer sine egne betingelser er fascinerende. Emnet hedder fyllotaksi eller Phyllotaxis på engelsk. Hos en solsikke består blomsterkurven af gule randblomster og i midten er der en mængde små mørke skiveblomster. Sidstnævnte danner et kompliceret spiralmønster,
både mod højre og mod venstre, som vist på figurerne nedenfor. Den spændende egenskab er, at antallet af højredrejede spiraler og venstredrejede spiraler næsten altid er Fibonacci-tal! I dette tilfælde kan man tælle 55 venstredrejede spiraler og 34 højredrejede spiraler! Klik eventuelt på hver af billederne for at få en større version!

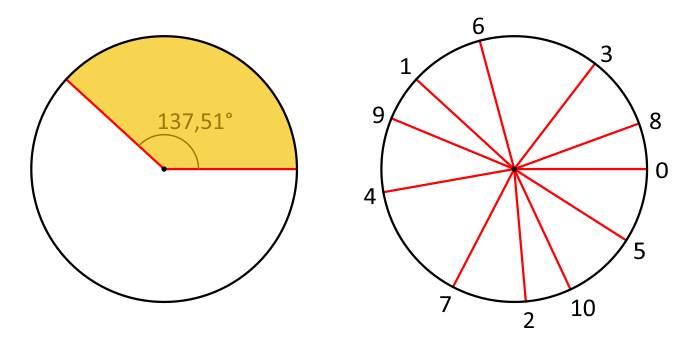
Helmut Vogel fra Technische Universität München publiserede i 1979 en artikel i tidsskriftet Mathematical Biosciences (se [26]) en model, for skiveblomsternes indbyrdes placering i en solsikke. Idéen er, at der under væksten hele tiden skabes nye skiveblomster fra centrum af solsikken på en sådan måde, så de nye skiveblomster dannes eller fremkommer i en vinkel på ca. 137,5 grader i forhold til den forrige skiveblomst, regnet fra midten af solsikken. Den angivne vinkel viser sig at
have noget med det gyldne snit φ at gøre. Vinklen kaldes for den gyldne vinkel og er defineret, som det fremgår af boksen nedenfor.

Boksen ovenfor indeholder også den polære og rektangulære parameterfremstilling for skiveblomsternes placering (her er (0,0) antaget at være centrum af solsikkens blomst). Ved hjælp af et CAS-værktøj kan man, som jeg selv har gjort her i programmet Maple, fremstillet plots af 600 punkter, svarende til 600 skiveblomster). Den venstre del af figuren viser alle de 600 punkter ensfarvet. Man aner en form for spiraler i mønsteret! I den midterste del af figuren er hver anden højredrejet spiral farvet rød og hver anden højredrejet spiral farvet grøn, mens den højre del af figuren har hver anden venstredrejet spiral farvet blå og hver anden venstredrejet spiral farvet magenta. Hvis man tæller spiraler, opdager man til sin overraskelse, at der er 34 højredrejede spiraler og 55 venstredrejede spiraler, begge Fibonacci-tal! Klik evt. på billedet for en større version!
Ifølge Vogels model anbringes det nye punkt altid på en linje, som er drejet med den gyldne vinkel på ca. 137,51° i forhold til det forrige punkt. En af de vigtige pointer her er, at når man gentager denne vinkel gang efter gang, så vil man aldrig opnå et punkt på samme radie ud fra centrum! På den højre del af figuren nedenfor er processen gennemført for 10 gentagne drejninger med den gyldne vinkel. Begrundelsen for påstanden er, at kravet til at et punkt opnår samme vinkel som et forrigt punkt er, at den gentagne drejningsvinkel er et rationalt tal! (Overvej). Men det gyldne snit er som bekendt et irrationalt tal, endda i en vis forstand det "mest irrationale tal", nemlig det irrationale tal, som dårligst lader sig approksimere med rationale tal, ifølge afsnit 7. Derfor er den gyldne vinkel også et irrationalt tal.
Punkterne i Vogels model anbringes netop i retninger angivet ved gentagne drejninger med den gyldne vinkel. Afstanden vokser dog med kvadratroden af k, hvor k er punktets nummer i følgen. Det betyder, at de kommer til at ligge på en såkaldt Fermat spiral. Parameterfremstillingen for sidstnævnte fås ved i modellen at udskifte den diskrete parameter k med det reelle tal t. Der er en grund til at vælge netop kradratroden af k (eller et tal proportionalt med det) som radius. Det betyder nemlig lidt løst sagt, at antallet af punkter pr. areal vil nærme sig asymptotisk mod et konstant tal, når man betragter cirkler med større og større radius r centreret omkring origo (Overvej). En cirkel med radius r vil have et areal, som vokser med r2; derfor anbringer vi punkterne med en radius, som er kvadratroden af punktnummeret. Helmut Vogels idé lader sig måske bedst illustrere med en animation. I animationen nedenfor, hvor den underliggende Fermat-spiral også er aftagnet svagt, tegnes dog kun de første 100 punkter, hvorefter man kan se resultatet i ca. 10 sekunder, før animationen starter forfra ..
.
J. N. Ridley viste i en artikel fra Mathematical Biosciences, 1982 (se ([27]), at Helmut Vogels model giver anledning til den størst mulige paknings-effektivitet.
Det er klart, at skiveblomsterne i en rigtig solsikke ikke vokser ud i den rækkefølge, som Helmut Vogels model angiver. Skiveblomsterne dannes altid inde fra centrum af blomsten, mens de ældre skiveblomster vokser udefter. Det gør de i øvrigt radialt. Vogels model beskriver dermed ikke den tidsmæssige udvikling, kun skiveblomsternes placering. Et meget naturligt og vigtigt spørgsmål er herefter naturligvis, hvorfor en solsikkes skiveblomster vokser ud og danner det fine geometriske mønster, som den gør? Botanikeren Wilhelm Hofmeister studerede planters meristem i mikroskop. Han foreslog her, at et primordium (tidligst erkendelige forstadium til organ eller væv) altid dannes på det mindst fyldte sted omkring meristem (se [28]). Det bliver omtalt som Hofmeisters regel. Meristem betyder her det område i planten, hvor cellerne vedvarende deler sig. Bogen [28] omtaler også en dynamisk model (af Atela, Golé og Hotton fra 2002), som tager udgangspunkt i Hofmeisters regel. Forfatterne til artiklen pointerer, at det forekommer, at de observerede Fibonacci-lignende spiraler, som skiveblomsterne danner, og den gyldne vinkel kan være dikteret af et behov for meristem for at pakke primodia effektivt, når de er i et overfyldt område. Der forskes stadig i dette område.
Lad os lige slutte af med at vise, hvor meget anderledes punkterne i Helmut Vogels model fordeler sig, hvis man anvender en anden drejningsvinkel v end den gyldne vinkel.
Vi har tilfældet med den gyldne vinkel i midten. Her fordeler punkterne sig utroligt fint arealmæssigt. Til venstre for har vi en vinkel, som blot er en smule større. Alligevel bliver resultatet en del anderledes. Punkterne klumper mere sammen visse steder. I tilfældet til højre, hvor vinklen er det pæne tal 140°, er der en tydelig periodicitet i de vinkler, hvori der forekommer punkter. Gentages vinklen 18 gange, er man ved udgangspunktet: 18 gange 140° giver det samme som 7 gange 360°. Vi ser her stor ophobning af punkter i de 18 forskellige vinkler: 0, 20, 40, 60, ... , 340 grader.
Også hos ananas kan man se et lignende fænomen. Her er hvert af de hexagonale skæl på frugtens overflade faktisk en del af hele tre forskellige spiraler! Igen er antallet altid et Fibonacci-tal! Vi skal ikke gå mere i detaljer med det her.
Et andet eksempel er et romanesco kål (eller romanasco broccoli). Her har blomsterstanden en struktur, som minder om en selvsimilær fraktal. De små "buketter" (meristem) danner en logaritmisk spiral. I hver af de små buketter gentager strukturen sig, bare i en mindre målestok. Der er selvfølgelig kun tale om en approksimativ fraktal struktur, for det selvsimilære mønster gentager sig ikke uendeligt, men stopper, når buketterne er blevet tilstrækkelig små.
Antallet
af spiraler på et romanesco kålhoved er et Fibonacci-tal, ligesom det var tilfældet med solsikken.
Det nævnes undertiden, at sneglehuset Nautilus danner en del af en gylden spiral (se definition i afsnit 5). Det er imidlertid forkert. Dog kan man sige, at den er en approksimativ logaritmisk spiral.

|
[L1] |
https://en.wikipedia.org/wiki/Pythagoras (Om Pythagoras på Wikipedia) |
|
[L2] |
https://en.wikipedia.org/wiki/Pythagoreanism (Om pythagoræerne på Wikipedia) |
|
[L3] |
https://www.musikipedia.dk/stemningssystemer (Musikipedia. En glimrende gennemgang af de forskellige musikalske stemninger, begyndende med den pythagoræiske). |
|
[L4] |
https://projekter.aau.dk/projekter/files/261556875/Kandidatspeciale.pdf (En meget fin matematisk beskrivelse af stemningssystemer af Sara Scully i hendes kandidatspeciale). |
|
[L5] |
https://aktuelnaturvidenskab.dk/fileadmin/Aktuel_Naturvidenskab/nr-2/an2-1999fysik-musik.pdf (Fysik og Musik i videnskabshistorien fra tidsskriftet Aktuel Naturvidenskab, 2/1999) |
|
[L6] |
https://www.math.uwaterloo.ca/~mrubinst/tuning/12.html (Why 12 Notes to an Octave) |
|
[L7] |
http://www.stat.yale.edu/~zf59/MathematicsOfMusic.pdf (Zhou Fan: Seminar Notes: The Mathematics of Music. |
|
[L8] |
https://www.goldennumber.net/ (En god side om det Gyldne snit) |
|
[L9] |
https://www.youtube.com/watch?time_continue=447&v=0vVxL60YFJU&feature=emb_logo (The (absurd) Golden Ratio, YouTube video ved Robb Enzmann). |
|
[L9] |
https://www.youtube.com/watch?time_continue=4&v=O2wU-HT7FiM&feature=emb_logo (Fibonacci and the Golden Section). |
|
[L10] |
https://vimeo.com/9953368 (Nature by Numbers - fantastisk flot grafisk). |
|
[1] |
Jesper Lützen. Cirklens kvadratur, Vinklens tredeling, Terningens fordobling. Fra oldtidens geometri til moderne algebra. Systime, 1985. |
|
[2] |
Jonny Schultz, Hans Sloth (redaktører). Euklid: Elementer I-IV. Forlaget TRIP, 1994 (Oversættelser af Euklids Elementer ved Thyra Eibe). |
|
[3] |
Kirsti Andersen, Mikkel Vestergaard Laursen. Ikke alle skæringer er gyldne. En artikel i LMFK-bladet 4, 2011. |
|
[4] |
Olaf Pedersen. Matematik og Naturbeskrivelse i Oldtiden. Akademisk forlag, 1980 (oprindeligt 1975). |
|
[5] |
Asger Aaboe. Episoder fra matematikkens historie. 2. udgave. Borgens forlag, 1986. |
|
[6] |
Victor J. Katz. A History of Mathematics – An Introduction. 3rd Edition, Addison-Wesley, 2009. |
|
[7] |
Sir Thomas Heath. A History of Greek Mathematics. Volume I, From Thales to Euclid. Dover Publications Inc., 1981 (opr. 1921) |
|
[8] |
A. Beutelspacher, B. Petri. Der Goldene Schnitt. 2. Auflage. Wissenschaftsverlag, 1995. |
|
[9] |
Mario Livio. The Golden Ratio – The Story of Phi, the World's Most Astonishing Number. Broadway Books, 2002. |
|
[10] |
Gary B. Meisner. The Golden Ratio: The Divine Beauty of Mathematics. Race Point Publishing, 2018. |
|
[11] |
Scott Olsen. The Golden Section: Nature's Greatest Secret. Bloomsbury, 2006. |
|
[12] |
Claus Glunk, Hanne E. Strand, Chr. Marinus Taisbak, Chr. Gorm Tortzen. Q.E.D. Platon og Euklid tegner og fortæller. Gyldendal 2006. |
|
[13] |
Peter Kjeldsen, Mogens Nørgaard Olesen. Vort solsystem - En matematisk, filosofisk og astronomisk fortælling om solsystemets indretning. Systime, 1984. |
|
[14] |
Gert Uttenthal Jensen. Tal og tangenter - Om matematikken og musikken bag at stemme et klaver. 2. udgave. Matematikforlaget, 2012. |
|
[15] |
John Fauvel, Raymond Flood, Robin Wilson (Editors). Music and Mathematics - From Pythagoras to Fractals. Oxford University Press, 2006 (opr. 2003). |
|
[16] |
Thomas Heath (Translation), Dana Densmore (Editor). Euclid's Elements - all thirteen books complete in one volume. Green Lion Press, 2017 (opr. 2002). |
|
[17] |
Sir Thomas L. Heath. A Manual of Greek Mathematics. Dover Publications Inc., 2003 (opr. 1931) |
|
[18] |
Hans Buhl. Sfærernes harmoni - en videnskabshistorie om forholdet mellem musik og fysik. Steeno Museets Venner, 2000. |
|
[19] |
Jesper Lützen. Cirklens kvadratur, Vinklens tredeling, Terningens fordobling - Fra oldtidens geometri til moderne algebra. Systime, 1985. |
|
[20] |
Euklid (oversat til dansk af Tyra Eibe). Euklid: Elementer I-IV. Forlaget TRIP, 1994. |
|
[21] |
Alexander J. Hahn. Mathematical Excursions to the World's Great Buildings. Princeton University Press, 2012. |
|
[22] |
Mario Livio. Det gyldne snit. Nyt Teknisk Forlag, 2004. (Oversættelse af engelsk udgave) |
|
[23] |
Heinrich Dörrie (Tranlated by David Antin). 100 Great problems of Elementary Mathematics - Their History and solution). Dover Publications, 1965 (opr. 1958). |
|
[24] |
Gert M. Flensberg. Geometriske konstruktioner. Systime, 1983. |
|
[25] |
H. S. M. Coxeter. Introduction to Geometry. John Wiley and Sons, Inc. (Wiley Classics Library Edition Published 1989). Opr. 1961. |
|
[26] |
Helmut Vogel. A better Way to Construct the Sunflower Head. Mathematical Biosciences 44, p. 179-189 (1979). |
|
[27] |
J. N. Ridley. Packing Efficiency in Sunflower Heads. Mathematical Biosciences 58, p. 129-139 (1982). |
|
[28] |
K. K. Tung. Topics in Mathematical Modeling. Princeton University Press, 2007. |
|
[29] |
Przemyslaw Prusinkiewicz, Aristid Lindenmayer. The Algorithmic Beauty of Plants. Springer-Verlag, 1990. |
Opdateret 16.01.20
|
|